GRASS GIS manual: r.stream.order

NAME

r.stream.order - Calculate Strahler's and Horton's stream order Hack's main streams and Shreeve's stream magnitude. It use r.watershed or r.stream.extract output files: stream, direction and optionally accumulation. Output data can be either from r.watershed or r.stream.extract but not from both together

KEYWORDS

stream, order, magnitude, Horton, Strahler, Shreeve

SYNOPSIS

r.stream.order
r.stream.order help
r.stream.order [-z] stream=string dir=string [table=string] [accum=string] [strahler=string] [shreve=string] [horton=string] [hack=string] [topo=string] [--overwrite] [--verbose] [--quiet]

Flags:

-z: Create zero-value background instead of NULL
--overwrite: Allow output files to overwrite existing files
--verbose: Verbose module output
--quiet: Quiet module output

Parameters:

stream=string: Name of stream mask input map (r.watershed or r.stream.extract)
dir=string: Name of direction input map (r.watershed or r.stream.extract)
table=string: Name of new table to create
accum=string: (Not recommended) Name of accumulation file (r.watershed or r.stream.extract)
strahler=string: Name of Strahler's stream order output map
shreve=string: Name of Shreve's stream magnitude output map
horton=string: Name of Horton's stream order output map
hack=string: Name of Hack's main streams output map
topo=string: Name of topological dimension output map

DESCRIPTION

OPTIONS

-z: Creates zero-value background instead of NULL. For some reason (like map algebra calculation) zero-valued background may be required. This flag produces zero-filled background instead of null (default).
stream: Stream network: name of input stream map on which ordering will be performed produced by r.watershed or r.stream.extract. Because streams network produced by r.watershed and r.stream.extract may slighty differ in detail it is required to use both stream and direction map produced by the same module. Stream background shall have NULL value or zero value. Background values of NULL are by default produced by r.watershed and r.stream.extract. If not 0 or NULL use r.mapcalc to set background values to null.
dir: Flow direction: name of input direction map produced by r.watershed or r.stream.extract. If r.stream.extract output map is used, it only has non-NULL values in places where streams occur. NULL (nodata) cells are ignored, zero and negative values are valid direction data if they vary from -8 to 8 (CCW from East in steps of 45 degrees). Direction map shall be of type CELL values. Region resolution and map resoultion must be the same. Also stream network and accumulation maps must have the same resolution. It is checked by default. If resolutions differ the module informs about it and stops. Region boundary and maps boundary may be differ but it may lead to unexpected results.
table: Table where stream network topology can be stored. Because r.stream.order is prepared to work both with r.watershed and r.stream.extract, table by default is not attached to vector, but if stream network is produced by r.stream.extract it can be simply added to file using v.db.connect. See DESCRIPTION for details
accum: Flow accumulation (optional, not recommended): name of flow accumulation file produced by r.watershed or used in r.stream.extract. This map is an option only if Horton's or Hack's ordering is performed. Normally both Horton and Hack ordering is calculated on cumulative stream lrngth which is calculated internaly. Flow accumulation can be used if user want to calculate main stream as most accumulated stream. Flow accumulation map shall be of DCELL type, as is by default produced by r.watershed or converted do DCELL with r.mapcalc.
strahler: Name of Strahler's stream order output map: see notes for detail.
shreve: Name of Shreve's stream magnitude output map: see notes for detail.
horton: Name of Horton's stream order output map (require accum file): see notes for detail.
hack: Name of Hack's main streams output map : see notes for detail.
top: Name of topological dimensions streams output map: see notes for detail.

Stream ordering example:

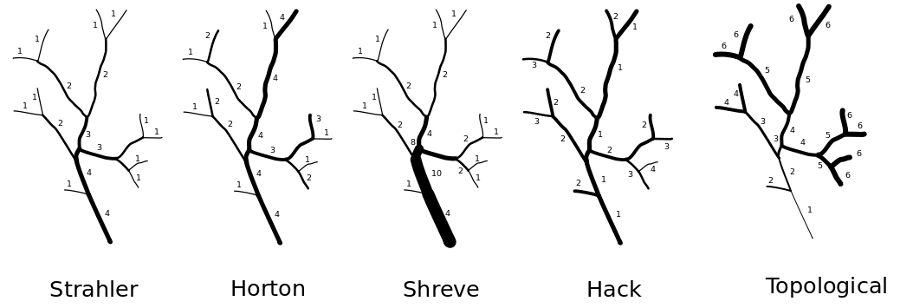
Strahler's stream order

Strahler's stream order is a modification of Horton's streams order which fixes the ambiguity of Horton's ordering. In Strahler's ordering the main channel is not determined; instead the ordering is based on the hierarchy of tributaries. The ordering follows these rules:

if the node has no children, its Strahler order is 1.
if the node has one and only one tributuary with Strahler greatest order i, and all other tributaries have order less than i, then the order remains i.
if the node has two or more tributaries with greatest order i, then the Strahler order of the node is i + 1.

Strahler's stream ordering starts in initial links which assigns order one. It proceeds downstream. At every node it verifies that there are at least 2 equal tributaries with maximum order. If not it continues with highest order, if yes it increases the node's order by 1 and continues downstream with new order.
Advantages and disadvantages of Strahler's ordering: Strahler's stream order has a good mathematical background. All catchments with streams in this context are directed graphs, oriented from the root towards the leaves. Equivalent definition of the Strahler number of a tree is that it is the height of the largest complete binary tree that can be homeomorphically embedded into the given tree; the Strahler number of a node in a tree is equivalent to the height of the largest complete binary tree that can be embedded below that node. The disadvantage of that methods is the lack of distinguishing a main channel which may interfere with the analytical process in highly elongated catchments

Horton's stream order

Horton's stream order applies to the stream as a whole but not to segments or links since the order on any channel remains unchanged from source till it "dies" in the higher order stream or in the outlet of the catchment. The main segment of the catchment gets the order of the whole catchment, while its tributaries get the order of their own subcatchments. The main difficulties of the Horton's order are criteria to be considered to distinguish between "true" first order segments and extension of higher order segments. That is the reason why Horton's ordering has rather historical sense and is substituted by the more unequivocal Strahler's ordering system. There are no natural algorithms to order stream network according to Horton' paradigm. The algorithm used in r.stream.order requires to first calculate Strahler's stream order (downstream) and next recalculate to Horton ordering (upstream). To make a decision about proper ordering it uses first Strahler ordering, and next, if both branches have the same orders it uses flow accumulation to choose the actual link. The algorithm starts with the outlet, where the outlet link is assigned the corresponding Strahler order. Next it goes upstream and determines links according to Strahler ordering. If the orders of tributaries differ, the algorithm proceeds with the channel of highest order, if all orders are the same, it chooses that one with higher flow length rate or higher catchment area if accumulation is used. When it reaches the initial channel it goes back to the last undetermined branch, assign its Strahler order as Horton order and goes upstream to the next initial links. In that way stream orders remain unchanged from the point where Horton's order have been determined to the source.
Advantages and disadvantages of Horton's ordering: The main advantages of Horton's ordering is that it produces natural stream ordering with main streams and its tributaries. The main disadvantage is that it requires prior Strahler's ordering. In some cases this may result in unnatural ordering, where the highest order will be ascribed not to the channel with higher accumulation but to the channel which leads to the most branched parts of the the catchment.

Shreve's stream magnitude

That ordering method is similar to Consisted Associated Integers proposed by Scheidegger. It assigns magnitude of 1 for every initial channel. The magnitude of the following channel is the sum of magnitudes of its tributaries. The number of a particular link is the number of initials which contribute to it. To achive Consisted Associated Integers the result of Shreve's magnitude is to be multiplied by 2:

r.mapcalc scheidegger=shreve*2 The algorithm is very similar to Strahler's algorithm, it proceeds downstream, and at every node the stream magnitude is the sum of its tributaries.

Hack's main streams order

This method of ordering calculates main streams of main catchment and every subcatchments. Main stream of every catchment is set to 1, and consequently all its tributaries receive order 2. Their tributaries receive order 3 etc. The order of every stream remains constant up to its initial link. The route of every main stream is determined according to the maximum flow length value of particular streams. So the main stream of every subcatchment is the longest stream or strean with highest accumulation rate if accumulation map is used. In most cases the main stream is the longest watercourse of the catchment, but in some cases, when a catchment consists of both rounded and elongated subcatchments these rules may not be maintained. The algorithm assigns 1 to every outlets stream and goes upstream according to maximum flow accumulation of every branch. When it reaches an initial stream it step back to the first unassigned confluence. It assigns order 2 to unordered tributaries and again goes upstream to the next initial stream. The process runs until all branches of all outlets are ordered.
Advantages and disadvantages of main stream ordering: The biggest advantage of that method is the possibility to compare and analyze topology upstream, according to main streams. Because all tributaries of main channel have order of 2, streams can be quickly and easily filtered and its proprieties and relation to main stream determined. The main disadvantage of that method is the problem with the comparison of subcatchment topology of the same order. Subcatchments of the same order may be both highly branched and widespread in the catchment area and a small subcatchment with only one stream.

Topological dimension streams order

This method of ordering calculates topological distance of every stream from catchment outlet. The topopological distance is defined as the number of segments which separates the current segment from the outlet basin

Stream network topology table description

cat integer: category;

streaminteger: stream number, usually equal to cat;

next_stream integer: stream to which contribute current stream (downstream);

prev_streams; two or more contributing streams (upstream);

strahler integer: Strahler's stream order:

horton integer: Hortons's stream order:

shreve integer: Shreve's stream magnitude;

hack integer: Hack's main streams order;

topo integer: Topological dimension streams order;

length double precision: stream length;

cum_length double precision: length of stream from source;

out_dist double precision: distance of current stream init from outlet;

stright double precision: length of stream as stright line;

fractal double precision: fractal dimention: stream length/stright stream length

NOTES

Module can work only if direction map, stream map and region map has same settings. It is also required that stream map and direction map come from the same source. For lots of reason this limitation probably cannot be omitted. This means if stream map comes from r.stream.extract also direction map from r.stream.extract must be used. If stream network was generated with MFD method also MFD direction map must be used. Nowadays f direction map comes from r.stream.extract must be patched by direction map from r.watershed. (with r.patch).

REFERENCES

Claps, P., Fiorentino, M., Oliveto, G., (1994), Informational entropy of fractal river networks, Journal of Hydrology, 187(1-2), 145-156 .
Hack, J., (1957), Studies of longitudinal stream profiles in Virginia and Maryland, U.S. Geological Survey Professional Paper, 294-B
Horton, R. E. (1945), Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology, Geological Society of America Bulletin 56 (3): 275-370
Shreve, R., Statistical Law of Stream Numbers, J. Geol., 74, (1966), 17-37.
Strahler, A. N. (1952), Hypsometric (area-altitude) analysis of erosional topology, Geological Society of America Bulletin 63 (11): 1117–1142
Strahler, A. N. (1957), Quantitative analysis of watershed geomorphology, Transactions of the American Geophysical Union, 8(6): 913–920.

AUTHORS

Jarek Jasiewicz, Markus Metz

Last changed: $Date$

Main index - raster index - Full index