Note: This document is for an older version of GRASS GIS that is outdated. You should upgrade, and read the current addon manual page.


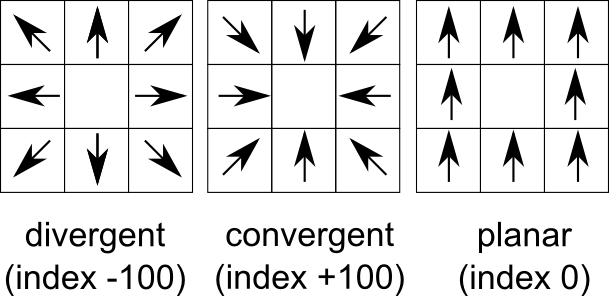
Convergence index is a terrain parameter which show the structure of the relief as a set of convergent areas (channels) and divergent areas (ridges). It represents the agreement of aspect direction of surrounding cells with the teoretical matrix direction. Convergence index is mean (or weighted mean if weights are used) aspect difference between real aspect and theoretical maximum divergent direction matrix representing ideal peak (see figure) minus 90 degres. So if there is maximum agreement with divergent matrix the convergence index is (0 - 90) * 10/9 = -100. If there is ideal sink (maximum convergence) the convergence index is (180 -90) * 10/9 = 100. Slope and aspect ere calculated internaly with the same formula as in r.slope.aspect. Convergence index is very useful for analysis of lineaments especially represented by rigdes or chanell systems as well as valley recognition tool.
Bauer J., Rohdenburg H., Bork H.-R., (1985), Ein Digitales Reliefmodell als Voraussetzung fuer ein deterministisches Modell der Wasser- und Stoff-Fluesse, IN: Bork, H.-R., Rohdenburg, H., Landschaftsgenese und Landschaftsoekologie, Parameteraufbereitung fuer deterministische Gebiets-Wassermodelle, Grundlagenarbeiten zu Analyse von Agrar-Oekosystemen, 1-15.
Böhner J., Blaschke T., Montanarella, L. (eds.) (2008). SAGA Seconds Out. Hamburger Beiträge zur Physischen Geographie und Landschaftsökologie, 19:113
Last changed: $Date: 2013-03-27 02:03:58 -0700 (Wed, 27 Mar 2013) $
Main index - raster index - Full index
© 2003-2014 GRASS Development Team