
NAME
r.fuzzy.set - Calculate membership value of any raster map according user's rules.KEYWORDS
raster, fuzzy logicSYNOPSIS
Flags:
- --overwrite
- Allow output files to overwrite existing files
- --help
- Print usage summary
- --verbose
- Verbose module output
- --quiet
- Quiet module output
- --ui
- Force launching GUI dialog
Parameters:
- input=name [required]
- Raster map to be fuzzified
- output=name [required]
- Membership map
- points=string[,string,...] [required]
- Inflection points: a,b[,c,d]
- Default: a,b[,c,d]
- side=string [required]
- Fuzzy range
- Options: both, left, right
- Default: both
- boundary=string [required]
- Type of fuzzy boundaries
- Options: Linear, S-shaped, J-shaped, G-shaped
- Default: S-shaped
- shape=float [required]
- Shape modifier: -1 to 1
- Options: -1, 1
- Default: 0.
- height=float [required]
- Membership height: 0 to 1
- Options: 0, 1
- Default: 1.
Table of contents
OPTIONS
- input
- Name of input raster map to be fuzzified. This map may be of any type and may require null values.
- points
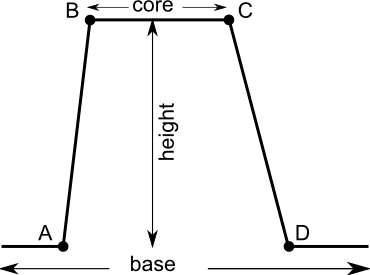
- A list containing 4 (A,B,C,D) or 2 A,B) points defining set boundaries.
Points must not to be in map range, but it may lead to only 0 o 1 membership for
the whole map. For "both" side parameters range between A and D defines base,
but range between B and C core of the fuzzy set. Between A and B and C and D are
set's boundaries. If side is "both" it require 4 points, else 2 points.
Fuzzy set definition:
- side
- Option indicate if set is fuzzified of both sides (both), left or right
side. See description for details.
Boundary definition:
OUTPUTS
- output
- Map containing membership value of original map. Map is alvays of type FCELLS and contains values from 0 (no membership) to 1 (full membership). Values between 0 and 1 indicate partial membership
FUZZY SET PARAMETERS
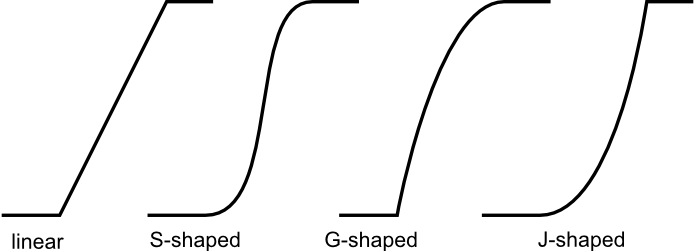
- boundary
- Parameter defined the shape of the fuzzy boundary. The default and most popular is S-shaped, linear, J-shaped and G-shaped boundaries are also available. The same boundaries are applied to the both sides.
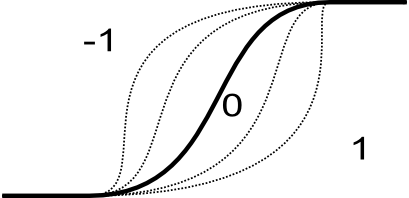
- shape
- Optional shape modifier. Range from -1 to 1. The default value is 0 and
should not be changed in most of the time. The negative values indicate more
dilatant set, the positive values more concentrate set. See description for
details.
Impact of shape parameter on shape boundary:
- height
- Optional height modifier. Range from 0 to 1. The default value is 1 and indicate full membership between points B and C. If height is lesser than one the maximum membership is equal to height. See image: Fuzzy set definition.
DESCRIPTION
Definition of fuzzy set
Fuzzy sets are sets whose elements have degrees of membership. Zadeh (1965) introduced Fuzzy sets as an extension of the classical notion of set. Classical membership of elements in a set are binary terms: an element either belongs or does not belong to the set. Fuzzy set theory use the gradual assessment of the membership of elements in a set. A membership function valued in the real unit interval [0, 1]. Classical sets, are special cases of the membership functions of fuzzy sets, if the latter only take values 0 or 1. Classical sets are in fuzzy set theory usually called crisp sets. The fuzzy set theory can be used in a wide range of domains in which information is imprecise, such as most of the GIS operations.NOTES
Calculation of boundary shape
Depending on type of the boundary different equation are used to determine its shape:
Linear: the membership is calculated according following equation:
value <= A -> x = 0
A< value > B -> x = (value-A)/(B-A)
B <= value >= C -> x = 1
C< value > D -> x = (D-value)/(D-C)
value >= D -> x = 0
where x: membership
S-shaped: it use following equation:
sin(x * Pi/2)^m (for positive shape parameter)
1-cos(x * Pi/2)^m (for negative shape parameter)
where x: membership, and
m = 2^exp(2,shape) (for positive shape parameter)
m = 2^(1+shape) (for negative shape parameter)
where m: shape parameter.
G-shaped and J shaped: it use following equations:
tan(x * Pi/4)^m (for J-shaped)
tan(x * Pi/4)^1/m (for G-shaped)
where x: membership, and
m = 2^exp(2,shape) (for positive shape parameter)
m = 2^(1+shape) (for negative shape parameter)
where m: shape parameter.
SEE ALSO
r.fuzzy.logic, r.mapcalc,REFERENCES
Zadeh, L.A. (1965). "Fuzzy sets". Information and Control 8 (3): 338–353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958.
Novák, Vilém (1989). Fuzzy Sets and Their Applications. Bristol: Adam Hilger. ISBN 0-85274-583-4.
Klir, George J.; Yuan, Bo (1995). Fuzzy sets and fuzzy logic: theory and applications. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-101171-5.
Klir, George J.; St Clair, Ute H.; Yuan, Bo (1997). Fuzzy set theory: foundations and applications. Englewood Cliffs, NJ: Prentice Hall. ISBN 0133410587.
Meyer D, Hornik K (2009a). \Generalized and Customizable Sets in R." Journal of Statistical Software, 31(2), 1{27. URL http://www.jstatsoft.org/v31/i02/.
Meyer D, Hornik K (2009b). sets: Sets, Generalized Sets, and Customizable Sets. R~package version~1.0, URL http://CRAN.R-project.org/package=sets.
AUTHOR
Jarek JasiewiczLast changed: $Date: 2014-07-09 11:48:15 +0200 (Wed, 09 Jul 2014) $
SOURCE CODE
Available at: r.fuzzy.set source code (history)
Main index | Raster index | Topics index | Keywords index | Graphical index | Full index
© 2003-2018 GRASS Development Team, GRASS GIS 7.4.1svn Reference Manual