---

NAME

r.convergence - Calculate convergence index.

KEYWORDS

raster, terrain

SYNOPSIS

r.convergence --help

OPTIONS

-s

Increase convergence if slope value is high. Slope parameter radically slow down computation time, especially if window parameter is high. If slope is used addational modifier is used according to formula: sin(current)*sin(target) + cos(current)*cos(target). if slope of current and target cells are equal. The modifier is 1. If not, the modifier is applied with formula: acos(cos(convergence) * modifier)

-c

use circular window instead of suqare (default)

input

Digital elevation model. Data can be of any type and any projection. To calculate relief convergnece, r.convergence uses real distance which is recalculated into cell distance, according formula:
distance_between_current_cell_and_traget_cell/distance_between_current_cell_and_nearest_neighbour_cell. It is important if convergence is calculated for large areas in LatLong projecton.

weights

Parameter describing the reduction of the impact of the cell due to its distance, where distance in cells:

• standard:no decay
• inverse:distance modifier is calculated as 1/x
• power:distance modifier is calculated as 1/(x*x)
• power:distance modifier is calculated as 1/(x*x)
• gentle:distance modifier is calculated as 1/((1-x)/(1+x))

window

window size. Must be odd. For now there is no limits in window size. r.convergence uses window size instead of classical radius for compatibility with other GRASS programs.

output

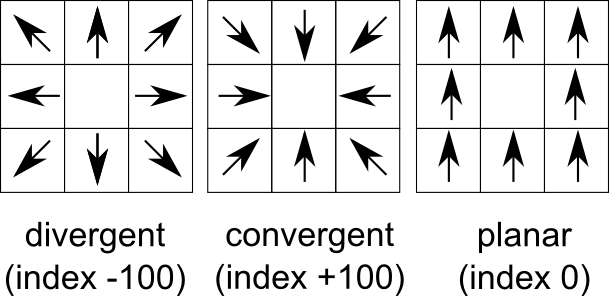
Map of convergence index. The values ranges from -100 (max divergent, real peaks and ridges) by 0 (planar areas) to 100 (max convergent, real pits and channels). Classical convergence index presented with degrees (-90 to 90)

DESCRIPTION

How convergence index is calculated (3 x 3 window):

Convergence index is a terrain parameter which show the structure of the relief as a set of convergent areas (channels) and divergent areas (ridges). It represents the agreement of aspect direction of surrounding cells with the teoretical matrix direction. Convergence index is mean (or weighted mean if weights are used) aspect difference between real aspect and teoretical maximum divergent direction matrix representing ideal peak (see figure) minus 90 degres. So if there is maximum agreement with divergent matrix the convergence index is (0 - 90) * 10/9 = -100. If there is ideal sink (maximum convergence) the convergence index is (180 -90) * 10/9 = 100. Slope and aspect ere calculated internaly with the same formula as in r.slope.aspect Convergence index is very useful for analysis of lineamets especially represented by rigdes or chanell systems as well as valley recognition tool.

SEE ALSO

r.slope.aspect, r.param.scale, r.neighbour,

REFERENCES

Claps, P., Fiorentino, M., Oliveto, G., (1994), Informational entropy of fractal river networks, Journal of Hydrology, 187(1-2), 145-156 .

Bauer J., Rohdenburg H., Bork H.-R., (1985), Ein Digitales Reliefmodell als Vorraussetzung fuer ein deterministisches Modell der Wasser- und Stoff-Fluesse, IN: Bork, H.-R., Rohdenburg, H., Landschaftsgenese und Landschaftsoekologie, Parameteraufbereitung fuer deterministische Gebiets-Wassermodelle, Grundlagenarbeiten zu Analyse von Agrar-Oekosystemen, 1-15.

Böhner J., Blaschke T., Montanarella, L. (eds.) (2008). SAGA Seconds Out. Hamburger Beiträge zur Physischen Geographie und Landschaftsökologie, 19: 113 s.

AUTHOR

Jarek Jasiewicz

Last changed: $Date: 2016-04-01 10:14:00 +0200 (Fri, 01 Apr 2016) $

SOURCE CODE

Available at: r.convergence source code (history)

---

Main index | Raster index | Topics index | Keywords index | Graphical index | Full index

© 2003-2019 GRASS Development Team, GRASS GIS 7.4.5svn Reference Manual