r.convergence - GRASS GIS manual

Note: This document is for an older version of GRASS GIS that will be discontinued soon. You should upgrade, and read the current manual page.

NAME

r.convergence - Calculate convergence index.

KEYWORDS

raster, terrain

SYNOPSIS

r.convergence

r.convergence --help

r.convergence [-cs] input=name output=name window=integer weights=string [--overwrite] [--help] [--verbose] [--quiet] [--ui]

Flags:

-c: Use circular window (default: square)
-s: Add slope convergence (radically slows down calculation time)
--overwrite: Allow output files to overwrite existing files
--help: Print usage summary
--verbose: Verbose module output
--quiet: Quiet module output
--ui: Force launching GUI dialog

Parameters:

input=name [required]: Digital elevation model map
output=name [required]: Output convergence index map
window=integer [required]: Window size; Default: 3
weights=string [required]: Method for reducing the impact of the cell due to distance; Options: standard, inverse, power, square, gentle; Default: standard

OPTIONS
DESCRIPTION
- How convergence index is calculated (3 x 3 window):
SEE ALSO
REFERENCES
AUTHOR

OPTIONS

-s

Increase convergence if slope value is high. Slope parameter radically slows down computation time, especially if the window parameter is high. If slope is used, a slope modifier is used according to the formula: sin(current)*sin(target) + cos(current)*cos(target). If the slope of current and target cells are equal, this modifier's value will be 1. The modifier is applied with the formula: acos(cos(convergence) * modifier)

-c

Use circular window instead of square (default)

input

Digital elevation model. Data can be of any type and any projection. To calculate relief convergence, r.convergence uses real distances which is recalculated into cell distance, according formula:
distance_between_current_cell_and_target_cell/distance_between_current_cell_and_nearest_neighbour_cell. It is important if convergence is calculated for large areas in Lat/Lon projection.

weights

Parameter describing the reduction of the impact of the cell due to its distance, where distance in cells:

standard: no decay
inverse: distance modifier is calculated as 1/x
power: distance modifier is calculated as 1/(x*x)
power: distance modifier is calculated as 1/(x*x)
gentle: distance modifier is calculated as 1/((1-x)/(1+x))

window

Window size. Must be odd. For now there are no limits in window size. r.convergence uses the window size instead of classical radius for compatibility with other GRASS GIS commands.

output

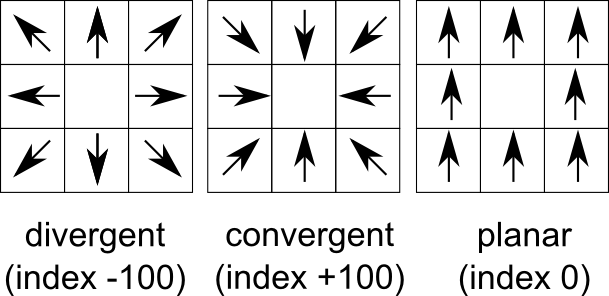
Map of convergence index. The values ranges from -100 (max divergent, real peaks and ridges) by 0 (planar areas) to 100 (max convergent, real pits and channels). Classical convergence index presented with degrees (-90 to 90)

DESCRIPTION

How convergence index is calculated (3 x 3 window):

Illustrations of convergence index values.
For divergent case, index is -100.
For convergent case, index is +100.
For planar case, index is 0.

Figure 1: Convergence index for maximum divergence, maximum convergence, and planar

Convergence index is a terrain parameter which shows the structure of the relief as a set of convergent areas (channels) and divergent areas (ridges). It represents the agreement of aspect direction of surrounding cells with the theoretical matrix direction. Convergence index is mean (or weighted mean if weights are used) aspect difference between real aspect and theoretical maximum divergent direction matrix representing ideal peak (see figure) minus 90 degrees. So if there is maximum agreement with divergent matrix the convergence index is (0 - 90) * 10/9 = -100. If there is ideal sink (maximum convergence) the convergence index is (180 -90) * 10/9 = 100. Slope and aspect are calculated internally with the same formula as in r.slope.aspect. Convergence index is very useful for analysis of lineaments especially represented by ridges or channel systems as well as valley recognition tool.

REFERENCES

Claps, P., Fiorentino, M., Oliveto, G., (1994), Informational entropy of fractal river networks, Journal of Hydrology, 187(1-2), 145-156 .

Bauer J., Rohdenburg H., Bork H.-R., (1985), Ein Digitales Reliefmodell als Vorraussetzung fuer ein deterministisches Modell der Wasser- und Stoff-Fluesse, IN: Bork, H.-R., Rohdenburg, H., Landschaftsgenese und Landschaftsoekologie, Parameteraufbereitung fuer deterministische Gebiets-Wassermodelle, Grundlagenarbeiten zu Analyse von Agrar-Oekosystemen, 1-15.

Böhner J., Blaschke T., Montanarella, L. (eds.) (2008). SAGA Seconds Out. Hamburger Beiträge zur Physischen Geographie und Landschaftsökologie, 19: 113 s.

AUTHOR

Jarek Jasiewicz

SOURCE CODE

Available at: r.convergence source code (history)

Latest change: Monday Jan 30 19:52:26 2023 in commit: cac8d9d848299297977d1315b7e90cc3f7698730