v.qcount - GRASS GIS manual

Note: This document is for an older version of GRASS GIS that will be discontinued soon. You should upgrade, and read the current manual page.

NAME

v.qcount - Indices for quadrat counts of vector point lists.

KEYWORDS

vector, statistics, point pattern

SYNOPSIS

v.qcount

v.qcount --help

v.qcount [-g] input=name [layer=string] [output=name] nquadrats=integer radius=float [--overwrite] [--help] [--verbose] [--quiet] [--ui]

Flags:

-g: Print results in shell script style
--overwrite: Allow output files to overwrite existing files
--help: Print usage summary
--verbose: Verbose module output
--quiet: Quiet module output
--ui: Force launching GUI dialog

Parameters:

input=name [required]: Name of input vector map; Or data source for direct OGR access
layer=string: Layer number or name ('-1' for all layers); A single vector map can be connected to multiple database tables. This number determines which table to use. When used with direct OGR access this is the layer name.; Default: -1
output=name: Name for output quadrat centers map (number of points is written as category)
nquadrats=integer [required]: Number of quadrats
radius=float [required]: Quadrat radius

DESCRIPTION
NOTES
KNOWN ISSUES
REFERENCES
SEE ALSO
AUTHORS

DESCRIPTION

v.qcount computes six different quadrat count statistics that provide a measure of how much an user defined point pattern departs from a complete spatial random point pattern.

Points are distributed following a complete spatial randomness (CSR) pattern if events are equally likely to occur anywhere within an area. There are two types departure from a CSR: regularity and clustering. Figure 1 gives an example of a complete random, regular and a clustered pattern.

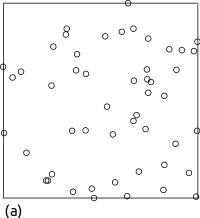
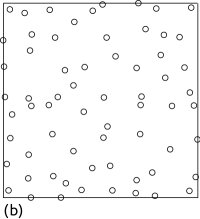
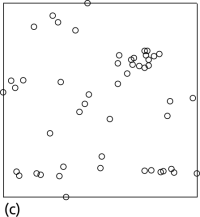
Figure 1: Realization of two-dimensional Poisson processes of 50 points on the unit square exhibiting (a) complete spatial randomness, (b) regularity, and (c) clustering.

Various indices and statistics measure departure from CSR. The v.qcount function implements six different quadrat count indices that are described in Cressie (1991; p. 590-591)[1] and in Ripley (1981; p. 102-106)[2] and summarized in Table 1.

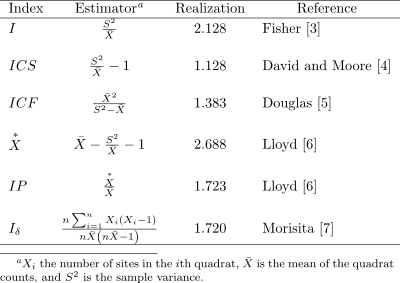
Table 1: Indices for Quadrat Count Data. Adapted from Cressie [1], this table shows the statistics computed for the quadrats in Figure 2.

These indices are computed as follows: v.qcount chooses nquadrads circular quadrats of radius radius such that they are completely within the bounds of the current region and no two quadrats overlap. The number of points falling within each quadrat are counted and indices are calculated to estimate the departure of point locations from complete spatial randomness. This is illustrated in Figure 2.

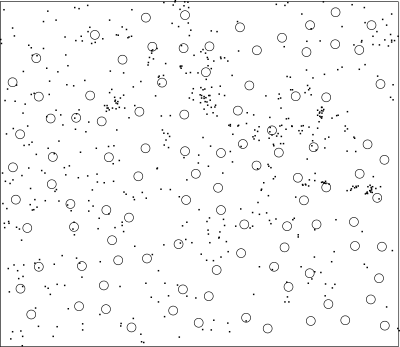
Figure 2: Randomly placed quadrats (n = 100) with 584 sample points.

The number of points is written as category to the output map (and not to an attribute table).

NOTES

This program may not work properly with lat-long data. It uses hypot() in two files: count.c and findquads.c.

KNOWN ISSUES

Timestamp not working for header part of counts output. (2000-10-28)

REFERENCES

General references include:

[1] Noel A. C. Cressie. Statistics for Spatial Data. Wiley Series in Probability and Mathematical Statistics. John Wiley & Sons, New York, NY, 1st edition, 1991.

[2] Brian D. Ripley. Spatial Statistics. John Wiley \& Sons, New York, NY, 1981.

References to the indices include:

[3] R. A. Fisher, H. G. Thornton, and W. A. Mackenzie. The accuracy of the plating method of estimating the density of bacterial populations. Annals of Applied Biology, 9:325-359, 1922.

[4] F. N. David and P. G. Moore. Notes on contagious distributions in plant populations. Annals of Botany, 18:47-53, 1954.

[5] J. B. Douglas. Clustering and aggregation. Sankhya B, 37:398-417, 1975.

[6] M. Lloyd. Mean crowding. Journal of Animal Ecology, 36:1-30, 1967.

[7] M. Morista. Measuring the dispersion and analysis of distribution patterns. Memoires of the Faculty of Science, Kyushu University, Series E. Biology, 2:215-235, 1959.

A more detailed background is given in the tutorial:

[8] James Darrell McCauley 1993. Complete Spatial Randomness and Quadrat Methods - GRASS Tutorial on v.qcount

AUTHORS

James Darrell McCauley
when he was at: Agricultural Engineering Purdue University

Modified for GRASS 5.0 by Eric G. Miller (2000-10-28)
Modified for GRASS 5.7 by R. Blazek (2004-10-14)

SOURCE CODE

Available at: v.qcount source code (history)

Latest change: Thursday Feb 03 11:10:06 2022 in commit: 547ff44e6aecfb4c9cbf6a4717fc14e521bec0be