NAME

KEYWORDS

SYNOPSIS

DESCRIPTION

In order to take into account the scale of the texture to be measured, r.texture allows the user to define the size of the moving window and the distance at which to compare pixel grey values. By default the module averages the results over the 4 orientations, but the user can also request output of the texture variables in 4 different orientations (flag -s). Please note that angles are defined in degrees of east and they increase counterclockwise, so 0 is East - West, 45 is North-East - South-West, 90 is North - South, 135 is North-West - South-East.

The user can either chose one or several texture measures (see below for their description) using the method parameter, or can request the creating of maps for all available methods with the -a.

r.texture assumes grey levels ranging from 0 to 255 as input. The input is automatically rescaled to 0 to 255 if the input map range is outside of this range. In order to reduce noise in the input data (thus generally reinforcing the textural features), and to speed up processing, it is recommended that the user recode the data using equal-probability quantization. Quantization rules for r.recode can be generated with r.quantile -r using e.g 16 or 32 quantiles (see example below).

NOTES

Texture is a feature of specific land cover classes in satellite imagery. It is particularly useful in situations where spectral differences between classes are small, but classes are distinguishable by their organisation on the ground, often opposing natural to human-made spaces: cultivated fields vs meadows or golf courses, palm tree plantations vs natural rain forest, but texture can also be a natural phenomen: dune fields, different canopies due to different tree species. The usefulness and use of texture is highly dependent on the resolution of satellite imagery and on the scale of the human intervention or the phenomenon that created the texture (also see the discussion of scale dependency below). The user should observe the phenomenon visually in order to determine an adequat setting of the size parameter.

The output of r.texture can constitute very useful additional variables as input for image classification or image segmentation (object recognition). It can be used in supervised classification algorithms such as i.maxlik or i.smap, or for the identification of objects in i.segment, and/or for the characterization of these objects and thus, for example, as one of the raster inputs of the i.segment.stats addon.

In general, several variables constitute texture: differences in grey level values, coarseness as scale of grey level differences, presence or lack of directionality and regular patterns. A texture can be characterized by tone (grey level intensity properties) and structure (spatial relationships). Since textures are highly scale dependent, hierarchical textures may occur.

r.texture uses the common texture model based on the so-called grey level co-occurrence matrix as described by Haralick et al (1973). This matrix is a two-dimensional histogram of grey levels for a pair of pixels which are separated by a fixed spatial relationship. The matrix approximates the joint probability distribution of a pair of pixels. Several texture measures are directly computed from the Grey Level Co-occurrence Matrix (GLCM). The provided measures can be categorized under first-order and second-order statistics, with each playing a unique role in texture analysis. First-order statistics consider the distribution of individual pixel values without regard to spatial relationships, while second-order statistics, particularly those derived from the Grey Level Co-occurrence Matrix (GLCM), consider the spatial relationship of pixels.

The following part offers brief explanations of the Haralick et al texture measures (after Jensen 1996).

First-order statistics in the spatial domain

• Sum Average (SA): Sum Average measures the average gray level intensity of the sum of pixel pairs within the moving window. It reflects the average intensity of pixel pairs at specific distances and orientations, highlighting the overall brightness level within the area.
• Entropy (ENT): This measure analyses the randomness. It is high when the values of the moving window have similar values. It is low when the values are close to either 0 or 1 (i.e. when the pixels in the local window are uniform).
• Difference Entropy (DE): This metric quantifies the randomness or unpredictability in the distribution of differences between the grey levels of pixel pairs. It is a measure of the entropy of the pixel-pair difference histogram, capturing texture granularity.
• Sum Entropy (SE): Similar to Difference Entropy, Sum Entropy measures the randomness or unpredictability, but in the context of the sum of the grey levels of pixel pairs. It evaluates the entropy of the pixel-pair sum distribution, providing insight into the complexity of texture in terms of intensity variation.
• Variance (VAR): A measure of gray tone variance within the moving window (second-order moment about the mean)
• Difference Variance (DV): This is a measure of the variance or spread of the differences in grey levels between pairs of pixels within the moving window. It quantifies the contrast variability between pixels, indicating texture smoothness or roughness.
• Sum Variance (SV): In contrast to Difference Variance, Sum Variance measures the variance of the sum of grey levels of pixel pairs. It assesses the variability in the intensity levels of pairs of pixels, contributing to an understanding of texture brightness or intensity variation.

Second-order statistics in the spatial domain

• Angular Second Moment (ASM, also called Uniformity): This is a measure of local homogeneity and the opposite of Entropy. High values of ASM occur when the pixels in the moving window are very similar.
  Note: The square root of the ASM is sometimes used as a texture measure, and is called Energy.
• Inverse Difference Moment (IDM, also called Homogeneity): This measure relates inversely to the contrast measure. It is a direct measure of the local homogeneity of a digital image. Low values are associated with low homogeneity and vice versa.
• Contrast (CON): This measure analyses the image contrast (locally gray-level variations) as the linear dependency of grey levels of neighboring pixels (similarity). Typically high, when the scale of local texture is larger than the distance.
• Correlation (COR): This measure analyses the linear dependency of grey levels of neighboring pixels. Typically high, when the scale of local texture is larger than the distance.
• Information Measures of Correlation (MOC): These measures evaluate the complexity of the texture in terms of the mutual dependence between the grey levels of pixel pairs. They quantify how one pixel value informs or correlates with another, offering insight into pattern predictability and structure regularity.
• Maximal Correlation Coefficient (MCC): This statistic measures the highest correlation between any two features of the texture, providing a single value that summarizes the degree of linear dependency between grey levels in the texture. It's often used to assess the overall correlation in the image, indicating how predictable the texture patterns are from one pixel to the next.

The computational region should be set to the input map with g.region raster=<input map>, or aligned to the input map with g.region align=<input map> if only a subregion should be analyzed.

Note that the output of r.texture will always be smaller than the current region as only cells for which there are no null cells and for which all cells of the moving window are within the current region will contain a value. The output will thus appear cropped at the margins.

Importantly, the input raster map cannot have more than 255 categories.

EXAMPLE

g.region raster=ortho_2001_t792_1m -p
# set grey level color table 0% black 100% white
r.colors ortho_2001_t792_1m color=grey
# extract grey levels
r.mapcalc "ortho_2001_t792_1m.greylevel = ortho_2001_t792_1m"
# texture analysis
r.texture ortho_2001_t792_1m.greylevel output=ortho_texture method=asm -s
# display
g.region n=221461 s=221094 w=638279 e=638694
d.shade color=ortho_texture_ASM_0 shade=ortho_2001_t792_1m

g.region -p raster=ortho_2001_t792_1m

# enter as one line or with \
r.quantile input=ortho_2001_t792_1m quantiles=16 -r | r.recode \
           input=ortho_2001_t792_1m output=ortho_2001_t792_1m_q16 rules=-

Second example: analysis of IDM (homogeneity) on a simple raster with North-South line pattern.

# import raster
r.in.ascii in=- output=lines << EOF
north: 9
south: 0
east: 9
west: 0
rows: 9
cols: 9
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 0 1 0
EOF

# adjust region to raster
g.region raster=lines

# calculate IDM (homogeneity) in all directions
r.texture -s lines method=idm output=text_lines

The following image shows the original map, the result in East-West direction and the result in North-South direction, showing how texture can depend on direction, with texture perfectly homogeneous (value=1) in the North-South direction, but quite heterogeneous in East-West direction, except for those areas where there are three columns of equal values (as size=3). The overlaid grid highlights that the texture measures output maps are cropped at the margins.

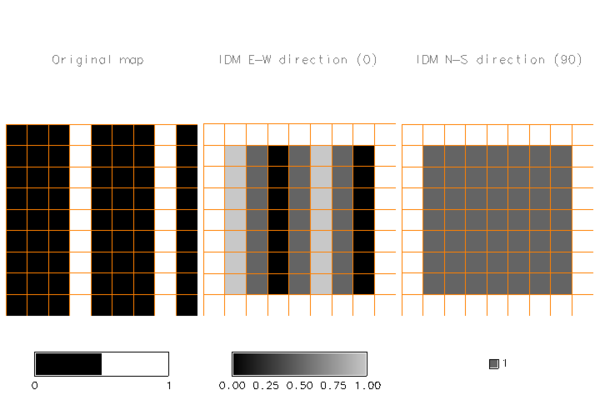
IDM textures according to direction

KNOWN ISSUES

REFERENCES

The original code was taken by permission from pgmtexture, part of PBMPLUS (Copyright 1991, Jef Poskanser and Texas Agricultural Experiment Station, employer for hire of James Darrell McCauley). Manual page of pgmtexture. Over the years, the source code of r.texture was further improved.

• Haralick, R.M., K. Shanmugam, and I. Dinstein (1973). Textural features for image classification. IEEE Transactions on Systems, Man, and Cybernetics, SMC-3(6):610-621.
• Bouman, C. A., Shapiro, M. (1994). A Multiscale Random Field Model for Bayesian Image Segmentation, IEEE Trans. on Image Processing, vol. 3, no. 2.
• Jensen, J.R. (1996). Introductory digital image processing. Prentice Hall. ISBN 0-13-205840-5
• Haralick, R. (May 1979). Statistical and structural approaches to texture, Proceedings of the IEEE, vol. 67, No.5, pp. 786-804
• Hall-Beyer, M. (2007). The GLCM Tutorial Home Page (Grey-Level Co-occurrence Matrix texture measurements). University of Calgary, Canada

SEE ALSO

AUTHORS

SOURCE CODE

Available at: r.texture source code (history)

Latest change: Tuesday Dec 17 20:17:20 2024 in commit: d962e90c026708a4815ea2b9f46c0e84c17de22d

Main index | Raster index | Topics index | Keywords index | Graphical index | Full index

© 2003-2024 GRASS Development Team, GRASS GIS 8.4.1dev Reference Manual