NAME

KEYWORDS

SYNOPSIS

OPTIONS

maps

A text file containing maps name and fuzzy sets connected with map definition. The input maps (indicated with % in text file) must be found in the search path. The output map name is the output name parameter. In map file output map is marked by special name _OUTPUT_ If maps are in different mapsets the name require @. Map names in database cannot contain following symbols: %,$ and #. Every map name must start with map name identifier: %. Every set definition connected with certain map must follow the map name and must start with set identifier : $. The set definition must be in braces { } and requires parameters separated by semicolon. Any whitespaces like spaces, tabs, empty lines are allowed and may used to visual format of rule file.

$ set_name {side; points; boundary_shape; hedge; height }

• set_name: Any name of the fuzzy set. Must not contain symbols: %,$ and #
• side: Option indicate if set is fuzzified of both sides (both), left or right side. Available: both, left, right.
• points: A list containing 4 (A,B,C,D) or 2 A,B) points separated by comma. Points define location of sets of boundaries. Points may not to be in map range, but it may lead to only 0 o 1 membership for the whole map. For "both" side parameters range between A and D defines base, but range between B and C core of the fuzzy set. Between A and B and C and D are set's boundaries. If side is "both" it require 4 points, else 2 points. Points values must be not-decreasing.
• shape: Parameter defined the shape of the fuzzy boundary. Available: sshaped, linear, jshaped, gshaped. The same boundaries are applied to both sides of fuzzy set.
• hedge: Shape modifier the positive number means dilatation (power the fuzzy set by 2) the negative means concentration (square root of fuzzy set). The number means number of dilatation/concentration applied on fuzzy set.
• height: Height modifier. Range from 0 to 1. The value 1 and indicate full membership between points B and C. If height is lesser than one the maximum membership is equal to height.

An example of fuzzy sets definition:

$ moderate {both; 90,100,120,130; sshaped; 0; 1}

Special notes about sets definition for output map:
These sets shall be created as triangular (both sides) sets with linear boundaries, without hedge and height modifiers:

$ moderate {both; 0,20,20,40; linear; 0; 1}

rules

A text file containing rules for classification.Th typical fuzzy rule consists of one or more antecedents and one consequent:

IF elev IS high AND distance IS low THEN probability IS small

where:
antecedents: elev IS high; distance IS low
consequent: probability IS small

The rule file has his own syntax. Because module creates only one result map, the map name is omitted. Every rule starts with $ and consist of consequent name and antecedents in braces { }. All maps and sets used in antecedents must be included in the maps file. At the beginning of the calculation program checks if all names and sets are included in maps file. Names of the rules must be same as sets names of the output map. The rules file use following symbols:

• IS is symbolised by =
• IS NOT is symbolised by ~
• AND is symbolised by &
• OR is symbolised by |
• To specify the order of operators must use parentheses ().

An example of fuzzy rules definition:

$ small {distance = high & elev = high}

ADVANCED OPTIONS

family

AND and OR operations in fuzzy logic are made with T-norms, T-conorms. T-norms, T-conorms are a generalization of the two-valued logical conjunction and disjunction used by boolean logic, for fuzzy logics. Because there is more than one possible generalisation of logical operations, r.fuzzy.system provides 6 most popular families for fuzzy operations:

• Zadeh with minimum (Godel) t-norm and maximum T-conorm;
• product with product T-norm and probabilistic sum as T-conorm;
• drastic with drastic T-norm and drastic T-conorm;
• Lukasiewicz with Lukasiewicz T-norm and bounded sum as a T-conorm;
• Fodor with nilpotent minimum as T-norm and nilpotent maximum as T-conorm;
• Hamacher (simplified) with Hamacher product as T-norm and Einstein sum as T-conorm;

Family	T-NORM (AND)	T CONORM (OR)
ZADEH	MIN(x,y)	MAX(x,y)
PRODUCT	x*y	x + y -x * y
DRASTIC	IF MAX(x, y) == 1 THEN MIN(x, y) ELSE 0	IF (MIN(x, y) == 0) THEN MAX(x, y) ELSE 1
LUKASIEWICZ	MAX((x+y-1),0)	MIN((x+y),1)
FODOR	IF (x+y)>1 THEN MIN(x,y) ELSE 0	IF (x+y<1) THEN MAX(x,y) ELSE 1
HAMACHER	IF (x==y==0) THEN 0 ELSE (x*y)/((x+y)-x*y)	(x+y)/(1+x*y)

imp: implication

Implication determines the method of reshapening of consequents (fuzzy set) by antecedents (single value) :

• minimum means the lowest value of the antecedents and output set definition. It usually creates trapezoidal consequent set definition.
• product means the multiplication of the antecedents and output set definition. It usually creates triangular consequent set definition.

defuzz: defuzzification method

Before defuzzification all consequents are aggregated into one fuzzy set. Defuzzification is the process of conversion of aggregated fuzzy set into one crisp value. The r.fuzzy.system provides 5 methods of defuzzification:

• centroid center of mass of the fuzzy set (in practise weighted mean);
• bisector a value which divide fuzzy set on two parts of equal area;
• min min (right limit) of highest part of the set;
• mean mean (center) of highest part of the set;
• max max (left limit) of highest part of the set;

res: universe resolution

The universe is an interval between the lowest and highest values of consequent and aggregated fuzzy sets. The resolution provides number of elements of these fuzzy sets. The minimum and maximum for universe is taken from the minimal and maximal values of fuzzy set definition of output map Because it has strong impact on computation time and precision of defuzzification, values lower than 30 may impact on precision of final result, but values above 200 may slow down computation time.

VISUAL OUTPUT

coordinates

Coordinates of points for which output: universe, all consequents sets and aggregate set. It is useful for visual presentation or detail analysis of fuzzy rules behaviour. In that cases calculations are performed n=only for selected point.

membership only flag

Prints for all maps sat of values in map range (map universe) and values of fuzzy sets (linguistic values). Number of values is taken from resolution (default 100). This option is useful for visual control fuzzy set definitions for every map.

OUTPUTS

output

Map containing defuzzified values. Map is always of type FCELLS and contains values defined in output universe. The output name must be the same as one of maps in maps definition file.

multiple output flag

This flag is used to create fuzzified maps for every rule. The name of the map consist of output map name, '_' and rule name (for example: output=probs and rule name high, the map name: probs_high). Values of maps ranges from 0 to 1. If map with such name exists will be overwritten without warning.

NOTES

Calculation of boundary shape

Linear: the membership is calculated according following equation:

value  <=  A -> x = 0
A< value > B -> x = (value-A)/(B-A)
B <= value >= C -> x = 1
C< value > D -> x = (D-value)/(D-C)
value  >=  D -> x = 0

sin(x * Pi/2)^2 (for S-shaped)
tan(x * Pi/4)^2 (for J-shaped)
tan(x * Pi/4)^0.5 (for G-shaped)

where:
x current fuzzy value
A,B,C,D inflection point,

EXAMPLE

Fuzzy sets are sets whose elements have degrees of membership. Zadeh (1965) introduced Fuzzy sets as an extension of the classical notion of set. Classical membership of elements in a set are binary terms: an element either belongs or does not belong to the set. Fuzzy set theory use the gradual membership of elements in a set. A membership function use values in the real unit interval [0, 1]. Classical sets, are special cases of the membership functions of fuzzy sets and only take values 0 or 1. Classical sets are in fuzzy set theory usually called crisp sets. The fuzzy set theory can be used in a wide range of domains in which information is imprecise, such as most of the GIS operations.

Suppose we want to determine the flood risk on some area (Spearfish dataset) using two maps: distance to streams and elevation above streams. We can write some common sense rules:

IF elevation IS low AND distance IS near THEN risk IS very probable
IF elevation IS low OR distance IS near THEN risk IS probable
IF elevation IS high AND distance IS far THEN risk IS unprobable

near: BELOW 100 = 1; FROM 100 TO 200 = {1 TO 0}; ABOVE 200 = 0;

First we need two maps created with r.stream package:

r.stream.extract elevation=elevation.10m threshold=2000 \
         stream_rast=streams direction=dirs
r.stream.order stream=streams dir=dirs horton=horton
r.mapcalc "horton3 = if(horton>2,horton,null())"
r.stream.distance stream=streams dir=dirs dem=elevation.10m method=downstream
distance=distance elevation=elevation 

MAPS Note: the raster map names are specified with a "%" character (here "%elevation" and "%distance" are the input maps and "%flood" the output map:

#flood.map
	%elevation
$ low {right; 2,6; sshaped; 0; 1}
$ high {left; 2,6; sshaped; 0; 1}
	%distance
$ near {right; 40,80; sshaped; 0; 1}
$ far {left; 40,80; sshaped; 0; 1}
#output map
	%flood
$ unprob {both; 0,20,20,40; linear; 0;1}
$ prob {both; 20,40,40,60; linear; 0;1}
$ veryprob {both; 40,60,60,80; linear; 0;1}

RULES:

#flood.rul
$ unprob {elevation = high & distance = far}
$ prob {distance = near | elevation = low}
$ veryprob {distance = near & elevation = low}

r.fuzzy.system maps=flood.map rules=flod.rul output=flood 

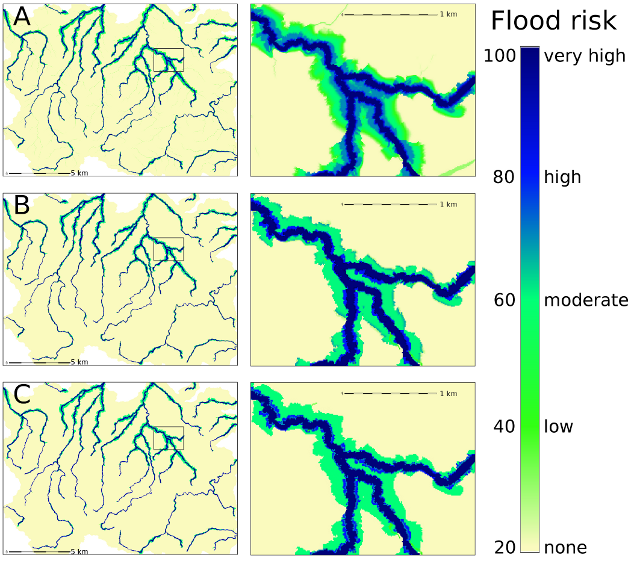
SEE ALSO

REFERENCES

Novák, Vilém (1989). Fuzzy Sets and Their Applications. Bristol: Adam Hilger. ISBN 0-85274-583-4.

Klir, George J.; Yuan, Bo (1995). Fuzzy sets and fuzzy logic: theory and applications. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-101171-5.

Klir, George J.; St Clair, Ute H.; Yuan, Bo (1997). Fuzzy set theory: foundations and applications. Englewood Cliffs, NJ: Prentice Hall. ISBN 0133410587.

Meyer D, Hornik K (2009a). \Generalized and Customizable Sets in R." Journal of Statistical Software, 31(2), 1{27. URL http://www.jstatsoft.org/v31/i02/.

Meyer D, Hornik K (2009b). sets: Sets, Generalized Sets, and Customizable Sets. R~package version~1.0, URL http://CRAN.R-project.org/package=sets.

AUTHOR

SOURCE CODE

Available at: r.fuzzy.system source code (history)

Main index | Raster index | Topics index | Keywords index | Graphical index | Full index

© 2003-2020 GRASS Development Team, GRASS GIS 7.8.3dev Reference Manual