GRASS logo

NAME

r.stream.order - Calculates Strahler's and more streams hierarchy.
Basic module for topological analysis of drainage network.

KEYWORDS

raster, hydrology, stream network, stream order

SYNOPSIS

r.stream.order
r.stream.order --help
r.stream.order [-zma] stream_rast=name direction=name [elevation=name] [accumulation=name] [stream_vect=name] [strahler=name] [horton=name] [shreve=name] [hack=name] [topo=name] [memory=integer] [--overwrite] [--help] [--verbose] [--quiet] [--ui]

Flags:

-z
Create zero-valued background instead of NULL
-m
Use memory swap (operation is slow)
-a
Use flow accumulation to trace horton and hack models
--overwrite
Allow output files to overwrite existing files
--help
Print usage summary
--verbose
Verbose module output
--quiet
Quiet module output
--ui
Force launching GUI dialog

Parameters:

stream_rast=name [required]
Name of input raster map with stream network
direction=name [required]
Name of input flow direction raster map
elevation=name
Name of input elevation raster map
accumulation=name
Name of input accumulation raster map
stream_vect=name
Name for output vector map to write stream attributes
strahler=name
Name for output Strahler's stream order raster map
horton=name
Name for output original Hortons's stream order raster map
shreve=name
Name for output Shereve's stream magnitude raster map
hack=name
Name for output Hack's streams or Gravelius stream hierarchy raster map
topo=name
Name for output topological dimension of streams raster map
memory=integer
Max memory used in memory swap mode (MB)
Default: 300

Table of contents

DESCRIPTION

The module r.stream.order calculates Strahler's and other stream hierarchy methods. It is a basic module for topological analysis of drainage networks.

NOTES

The module can work only if direction map, stream_rast map and the computational region have the same settings. It is also required that the stream_rast map and the direction map come from the same source. This means if stream_rast map comes from r.stream.extract also the direction map from r.stream.extract must be used. If stream network was generated with MFD method also MFD direction map must be used. Nowadays if direction map comes from r.stream.extract must be patched by direction map from r.watershed (with r.patch).

Input stream network map (stream_rast) may be produced using either r.watershed or r.stream.extract. Since stream network maps produced by r.watershed and r.stream.extract may slightly differ in detail, it is required to use both stream and direction maps produced by the same module. Non-stream cell values must be set to NULL.

Input direction raster map with flow direction may be produced using either r.watershed or r.stream.extract. If r.stream.extract output map is used, it is non-NULL only where streams occur and NULL elsewhere. NULL (nodata) cells are ignored, zero and negative values are valid direction data only if they vary from -8 to 8 (CCW from East in steps of 45 degrees). Flow direction map shall be of integer type (CELL).

Optional input flow accumulation map may be produced by r.watershed or r.stream.extract. This map is an option only if Horton's or Hack's ordering is performed. Normally both Horton and Hack ordering are calculated on cumulative stream length which is calculated internally. Flow accumulation can be used if the user wants to calculate the main channel as the stream with the highest value of accumulation. Flow accumulation map shall be of DCELL type, as is by default produced by r.watershed or converted to DCELL with r.mapcalc.

If -z is specified than r.stream.order creates zero-value background instead of NULL (no-data). For some reason (like map algebra calculation) zero-valued background may be required.

If -a is specified than r.stream.order uses accumulation raster map instead of cumulated stream length to determine main branch at bifurcation. Works well only with stream network produced with SFD algorithm.

Flag -m force to use segment library to optimise memory consumption during analysis. Recommended only for very large data sets.

Input elevation map can be of type CELL, FCELL or DCELL. It is used to calculate geometrical properties of the network stored in the table.

Output stream_vect vector map stores stream network. It has a table associated, where stream network topology can be stored. Because r.stream.order is prepared to work either with r.watershed or r.stream.extract, it may be used to create corrected stream vector from r.watershed results.

r.stream.order may produce various output raster maps strahler (Strahler's stream order raster map), shreve (Shreve's stream magnitude raster map), horton (Horton's stream order raster map - requires flow accumulation map), hack (Hack's stream order output raster map), and topo (topological dimension streams raster map).

Stream ordering example


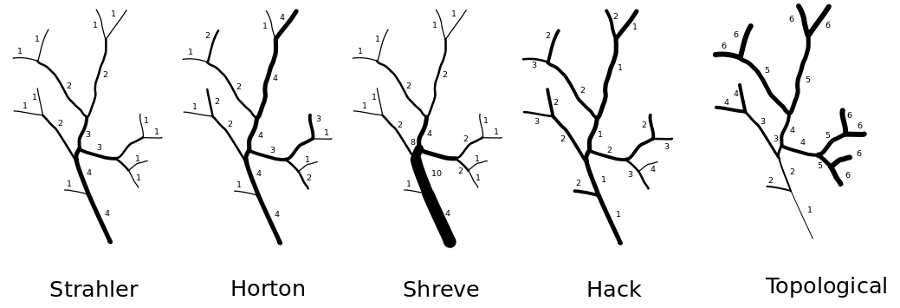
Strahler's stream order

Strahler's stream order is a modification of Horton's stream order which fixes the ambiguity of Horton's ordering. In Strahler's ordering the main channel is not determined; instead the ordering is based on the hierarchy of tributaries. The ordering follows these rules:
  1. if the node has no children, its Strahler order is 1.
  2. if the node has one and only one tributary with Strahler greatest order i, and all other tributaries have order less than i, then the order remains i.
  3. if the node has two or more tributaries with greatest order i, then the Strahler order of the node is i + 1.
Strahler's stream ordering starts in initial links which assigns order one. It proceeds downstream. At every node it verifies that there are at least 2 equal tributaries with maximum order. If not, it continues with the highest order; if yes, it increases the node's order by 1 and continues downstream with the new order.

Advantages and disadvantages of Strahler's ordering

Strahler's stream order has a good mathematical background. All catchments with streams in this context are directed graphs, oriented from the root towards the leaves. The equivalent definition of the Strahler number of a tree is that it is the height of the largest complete binary tree that can be homeomorphically embedded into the given tree; the Strahler number of a node in a tree is equivalent to the height of the largest complete binary tree that can be embedded below that node. The disadvantage of that methods is the lack of distinguishing a main channel which may interfere with the analytical process in highly elongated catchments

Horton's stream ordering

Horton's stream order applies to the stream as a whole but not to segments or links since the order on any channel remains unchanged from source till it "dies" in the higher order stream or in the outlet of the catchment. The main segment of the catchment gets the order of the whole catchment, while its tributaries get the order of their own subcatchments. The main difficulties of the Horton's order are the criteria to be considered to distinguish between "true" first order segments and extension of higher order segments. That is the reason why Horton's ordering has rather historical sense and is substituted by the more unequivocal Strahler's ordering system. There are no natural algorithms to order stream network according to Horton' paradigm. The algorithm used in r.stream.order requires to first calculate Strahler's stream order (downstream) and next recalculate to Horton ordering (upstream). To make a decision about proper ordering it uses first Strahler ordering, and next, if both branches have the same orders, it uses the flow accumulation to choose the actual link. The algorithm starts with the outlet, where to the outlet link is assigned the corresponding Strahler order. Next, it goes upstream and determines links according to Strahler ordering. If the orders of tributaries differ, the algorithm proceeds with the channel of highest order, if all orders are the same, it chooses that one with the higher flow length rate or the higher catchment area if the accumulation map is used. When it reaches the initial channel, it goes back to the last undetermined branch, assigns its Strahler order as Horton order and goes upstream to the next initial links. In that way stream orders remain unchanged from the point where Horton's order have been determined to the source.

Advantages and disadvantages of Horton's ordering

The main advantages of Horton's ordering is that it produces natural stream ordering with main streams and its tributaries. The main disadvantage is that it requires prior Strahler's ordering. In some cases this may result in unnatural ordering, where the highest order will be ascribed not to the channel with higher accumulation but to the channel which leads to the most branched parts of the catchment.

Shreve's stream magnitude

That ordering method is similar to Consisted Associated Integers proposed by Scheidegger. It assigns magnitude of 1 to every initial channel. The magnitude of the following channel is the sum of magnitudes of its tributaries. The number of a particular link is the number of initials which contribute to it.

Scheidegger's stream magnitude

That ordering method is similar to Shreve's stream magnitude. It assigns magnitude of 2 for every initial channel. The magnitude of the following channel is the sum of the magnitudes of its tributaries. The number of a particular link is the number of streams -1 contributing to it. Consisted Associated Integers (Scheidegger) is available only in attribute table. To achieve Consisted Associated Integers (Scheidegger) raster the result of Shreve's magnitude is to be multiplied by 2: 
r.mapcalc expr="scheidegger = shreve * 2.0"

Drwal's stream hierarchy (old style)

That ordering method is a compromise between Strahler ordering and Shreve magnitude. It assigns order of 1 for every initial channel. The order of the following channel is calculated according Strahler formula, except that streams which do not increase order of next channel are not lost. To increase next channel to the higher order R+1 are require two channels of order R, or one R and two R-1 or one R, and four R-2 or one R, one R-1 and two R-2 etc. The order of a particular link shows the possible value of Strahler'order if the network was close to idealised binary tree. Drwal's order is available only in attribute table.To achieve Drwal's raster the result of Shreve's magnitude is to be recalculated according to the formula: floor(log(shreve,2))+1 
r.mapcalc expr="drwal = int(log(shreve,2.0)) + 1.0"

Advantages and disadvantages of Drwal's hierarchy

The main advantages of Drwal's hierarchy is that it produces a natural stream ordering with which takes into advantage both ordering and magnitude. It shows the real impact of particular links of the network run-off. The main disadvantage is that it minimises the bifuraction ratio of the network.

Hack's main streams or Gravelius order

This method of ordering calculates main streams of the main catchment and every subcatchments. The main stream of every catchment is set to 1, and consequently all its tributaries receive order 2. Their tributaries receive order 3 etc. The order of every stream remains constant up to its initial link. The route of every main stream is determined according to the maximum flow length value of particular streams. So the main stream of every subcatchment is the longest stream or stream with highest accumulation rate if accumulation map is used. In most cases, the main stream is the longest watercourse of the catchment, but in some cases, when a catchment consists of both rounded and elongated subcatchments these rules may not be maintained. The algorithm assigns 1 to every outlets stream and goes upstream according to the maximum flow accumulation of every branch. When it reaches an initial stream, it steps back to the first unassigned confluence. It assigns order 2 to unordered tributaries and again goes upstream to the next initial stream. The process runs until all branches of all outlets are ordered.

Advantages and disadvantages of Hack's ordering

The biggest advantage of that method is the possibility to compare and analyze the topology upstream, according to the main streams. Because all tributaries of main channel have order of 2, the streams can be quickly and easily filtered and its properties and relation to main stream determined. The main disadvantage of that method is the problem with the comparison of subcatchment topology of the same order. Subcatchments of the same order may be both highly branched and widespread in the catchment area and a small subcatchment with only one stream.

Topological dimension streams order

This method of ordering calculates the topological distance of every stream from the catchment outlet.

Stream network topology table description connected with vector file

EXAMPLE

g.region -p -a raster=elevation
r.watershed elevation=elevation threshold=10000 drainage=direction stream=streams
r.stream.order stream_rast=streams direction=direction strahler=riverorder_strahler \
  horton=riverorder_horton shreve=riverorder_shreve hack=riverorder_hack \
  topo=river_topodim

# vector river network
r.watershed elevation=elevation threshold=10000 accumulation=accum
r.stream.order stream_rast=streams direction=direction elevation=elevation \
  accumulation=accum stream_vect=river_vector

REFERENCES

SEE ALSO

r.mapcalc, r.stream.channel, r.stream.distance, r.stream.extract, r.stream.segment, r.stream.slope, r.stream.snap, r.stream.stats, r.watershed

See also r.streams.* modules wiki page.

AUTHOR

Jarek Jasiewicz

SOURCE CODE

Available at: r.stream.order source code (history)

Main index | Raster index | Topics index | Keywords index | Graphical index | Full index

© 2003-2020 GRASS Development Team, GRASS GIS 7.8.3dev Reference Manual