r.fuzzy.system - GRASS GIS manual

Note: This document is for an older version of GRASS GIS that has been discontinued. You should upgrade, and read the current manual page.

NAME

r.fuzzy.system - Fuzzy logic classification system with multiple fuzzy logic families implication and defuzzification and methods.

KEYWORDS

raster, fuzzy logic

SYNOPSIS

r.fuzzy.system

r.fuzzy.system --help

r.fuzzy.system [-om] maps=name [rules=name] [family=string] [defuz=string] [imp=string] [res=integer] [coors=x,y] [output=name] [--overwrite] [--help] [--verbose] [--quiet] [--ui]

Flags:

-o: Print only membership values and exit
-m: Create additional fuzzy output maps for every rule
--overwrite: Allow output files to overwrite existing files
--help: Print usage summary
--verbose: Verbose module output
--quiet: Quiet module output
--ui: Force launching GUI dialog

Parameters:

maps=name [required]: Name of fuzzy variable file
rules=name: Name of rules file
family=string: Fuzzy logic family; Options: Zadeh, product, drastic, Lukasiewicz, Fodor, Hamacher; Default: Zadeh
defuz=string: Defuzzification method; Options: centroid, bisector, min_of_highest, max_of_highest, mean_of_highest; Default: bisector
imp=string: Implication method; Options: minimum, product; Default: minimum
res=integer: Universe resolution; Default: 100
coors=x,y: Coordinate of cell for detail data (print end exit)
output=name: Name of output file

OPTIONS
ADVANCED OPTIONS
VISUAL OUTPUT
OUTPUTS
NOTES
EXAMPLE
SEE ALSO
REFERENCES
AUTHOR

OPTIONS

maps file

A text file containing maps name and fuzzy sets connected with map definition. The input maps must be found in the search path. The output map name must be _OUTPUT_ If maps are in different mapsets the name requires @. Map names in database cannot contain the following symbols: %,$ and #. Every map name must start with map name identifier: %. Every set definition connected with certain map must follow the map name and must start with set identifier: $. The set definition must be in braces { } and requires parameters separated by semicolon. Any whitespaces like spaces, tabs, empty lines are allowed and may used to visual format of rule file. Lines beginning with # are comments.

$ set_name {side; points; boundary_shape; hedge; height }

set_name: Any name of the fuzzy set. Must not contain symbols: %,$ and #
side: Option indicate if set is fuzzified of both sides (both), left or right side. Available: both, left, right.
points: A list containing 4 (A,B,C,D) or 2 A,B) points separated by comma. Points define location of sets of boundaries. Points may not to be in map range, but it may lead to only 0 o 1 membership for the whole map. For "both" side parameters range between A and D defines base, but range between B and C core of the fuzzy set. Between A and B and C and D are set's boundaries. If side is "both" it require 4 points, else 2 points. Points values must be not-decreasing.
shape: Parameter defined the shape of the fuzzy boundary. Available: sshaped, linear, jshaped, gshaped. The same boundaries are applied to both sides of fuzzy set.
hedge: Shape modifier the positive number means dilatation (power the fuzzy set by 2) the negative means concentration (square root of fuzzy set). The number means number of dilatation/concentration applied on fuzzy set.
height: Height modifier. Range from 0 to 1. The value 1 and indicate full membership between points B and C. If height is lesser than one the maximum membership is equal to height.

An example of fuzzy sets definition:

$ moderate {both; 90,100,120,130; sshaped; 0; 1}

rules file

A text file containing rules for classification. A typical fuzzy rule consists of one or more antecedents and one consequent:

IF elev IS high AND distance IS low THEN probability IS small

where:
antecedents: elev IS high; distance IS low
consequent: probability IS small

The rule file has his own syntax. Because this module creates only one result map, the map name is omitted. Every rule starts with $ and consist of consequent name and antecedents in braces { }. Lines beginning with # are comments. All maps and sets used in antecedents must be included in the maps file. At the beginning of the calculation the program checks if all names and sets are included in maps file. Names of the rules must be same as the set names of the output map. The rules file uses the following symbols:

IS is symbolised by =
IS NOT is symbolised by ~
AND is symbolised by &
OR is symbolised by |
To specify the order of operators use parentheses ().

An example of fuzzy rules definition:

$ small {distance = high & elev = high}

ADVANCED OPTIONS

In most cases default options should not be changed.

family (fuzzy logic family)

AND and OR operations in fuzzy logic are made with T-norms and T-conorms. These are a generalization of the two-valued logical conjunction and disjunction used by boolean logic, for fuzzy logic. Because there is more than one possible generalisation of logical operations, r.fuzzy.system provides six common families for fuzzy operations:

Zadeh with minimum (Godel) t-norm and maximum T-conorm;
product with product T-norm and probabilistic sum as T-conorm;
drastic with drastic T-norm and drastic T-conorm;
Lukasiewicz with Lukasiewicz T-norm and bounded sum as a T-conorm;
Fodor with nilpotent minimum as T-norm and nilpotent maximum as T-conorm;
Hamacher (simplified) with Hamacher product as T-norm and Einstein sum as T-conorm;

Family T-NORM (AND) T CONORM (OR)

ZADEH MIN(x,y) MAX(x,y)

PRODUCT x*y x + y -x * y

DRASTIC IF MAX(x, y) == 1 THEN MIN(x, y) ELSE 0 IF (MIN(x, y) == 0) THEN MAX(x, y) ELSE 1

LUKASIEWICZ MAX((x+y-1),0) MIN((x+y),1)

FODOR IF (x+y)>1 THEN MIN(x,y) ELSE 0 IF (x+y<1) THEN MAX(x,y) ELSE 1

HAMACHER IF (x==y==0) THEN 0 ELSE (x*y)/((x+y)-x*y) (x+y)/(1+x*y)

imp (implication)

Family	T-NORM (AND)	T CONORM (OR)
ZADEH	MIN(x,y)	MAX(x,y)
PRODUCT	x*y	x + y -x * y
DRASTIC	IF MAX(x, y) == 1 THEN MIN(x, y) ELSE 0	IF (MIN(x, y) == 0) THEN MAX(x, y) ELSE 1
LUKASIEWICZ	MAX((x+y-1),0)	MIN((x+y),1)
FODOR	IF (x+y)>1 THEN MIN(x,y) ELSE 0	IF (x+y<1) THEN MAX(x,y) ELSE 1
HAMACHER	IF (x==y==0) THEN 0 ELSE (xy)/((x+y)-xy)	(x+y)/(1+x*y)

Implication determines the method of reshapening of consequents (fuzzy set) by antecedents (single value) :

minimum means the lowest value of the antecedents and output set definition. It usually creates trapezoidal consequent set definition.
product means the multiplication of the antecedents and output set definition. It usually creates triangular consequent set definition.

defuz (defuzzification method)

Before defuzzification all consequents are aggregated into one fuzzy set. Defuzzification is the process of conversion of aggregated fuzzy set into one crisp value. The r.fuzzy.system provides 5 methods of defuzzification:

centroid center of mass of the fuzzy set (in practise weighted mean);
bisector a value which divide fuzzy set on two parts of equal area;
min min (right limit) of highest part of the set;
mean mean (center) of highest part of the set;
max max (left limit) of highest part of the set;

res (universe resolution)

The universe is an interval between the lowest and highest values of consequent and aggregated fuzzy sets. The resolution provides number of elements of these fuzzy sets. The minimum and maximum for universe is taken from the minimal and maximal values of fuzzy set definition of output map Because it has strong impact on computation time and precision of defuzzification, values lower than 30 may impact on precision of final result, but values above 200 may slow down computation time.

VISUAL OUTPUT

coordinates: Coordinates of points for which output: universe, all consequents sets and aggregate set. It is useful for visual presentation or detail analysis of fuzzy rules behaviour. In that cases calculations are performed n=only for selected point.
membership only flag: Prints for all maps the set of values in the map range (map universe) and values of fuzzy sets (linguistic values). The number of values is taken from the resolution (default 100). This option is useful for visual control fuzzy set definitions for every map.

OUTPUTS

output (raster map): Map containing defuzzified values. Map is always of type FCELLS and contains values defined in output universe. The output name must be the same as one of maps in maps definition file.
multiple output flag: This flag is used to create fuzzified maps for every rule. The name of the map consist of output map name, '_' and rule name (for example: output=probs and rule name high, the map name: probs_high). Values of maps ranges from 0 to 1. If map with name exists it will be overwritten without warning.

NOTES

Calculation of boundary shape

Depending on the type of the boundary, different equations are used to determine the shape:

Linear: the membership is calculated according to the following equation:

value  <=  A -> x = 0
A< value > B -> x = (value-A)/(B-A)
B <= value >= C -> x = 1
C< value > D -> x = (D-value)/(D-C)
value  >=  D -> x = 0

S-shaped, G-shaped and J shaped: the following equation is used to smooth the boundary:

sin(x * Pi/2)^2 (for S-shaped)
tan(x * Pi/4)^2 (for J-shaped)
tan(x * Pi/4)^0.5 (for G-shaped)

where:
x current fuzzy value
A,B,C,D inflection point,

EXAMPLE

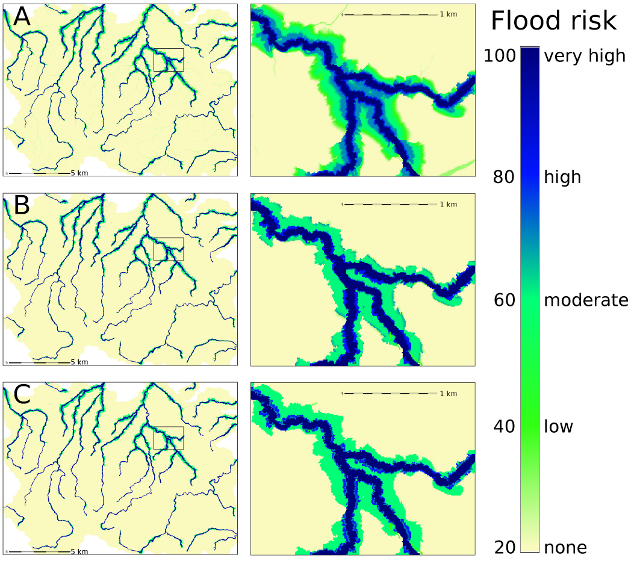
Fuzzy sets are sets whose elements have degrees of membership. Zadeh (1965) introduced Fuzzy sets as an extension of the classical notion of sets. Classical membership of elements in a set are binary terms: an element either belongs or does not belong to the set. Fuzzy set theory use the gradual assessment of the membership of elements in a set. A membership function valued in the real unit interval [0, 1]. Classical sets, are special cases of the membership functions of fuzzy sets, if the latter only take values 0 or 1. Classical sets are in fuzzy set theory usually called crisp sets. Fuzzy set theory can be used in a wide range of domains in which information is imprecise, including many GIS operations.

Suppose we want to determine the flood risk on some area (Spearfish dataset) using two maps: distance to streams and elevation above streams. We can write some common sense rules:

IF elevation IS low AND distance IS near THEN risk IS very probable
IF elevation IS low OR distance IS near THEN risk IS probable
IF elevation IS high AND distance IS far THEN risk IS unprobable

In classical boolean sense, we would taken some limits of ideas "near" "far" etc, but what about values near the limit? The fuzzy set uses partial memberships which abolish these restrictions. For example, the set "near" belongs all areas with distance no more than 100 m with full membership and from 100 to 200 m with partial membership greater than 0. Over 200 m we can assume that is not near. This allow the formulation of fuzzy rules for a distance map:

near: BELOW 100 = 1; FROM 100 TO 200 = {1 TO 0}; ABOVE 200 = 0;

To estimate the final map, the program calculates the partial fuzzy set for all rules and then aggregates it into one fuzzy set. These fuzzy sets are created on a value sequence called the "universe". Every set has the number of elements equal to the universe resolution. Such a set cannot be stored as a map so the set is defuzzified with a method chosen by user.

First we need two maps created with r.stream package:

r.stream.extract elevation=elevation.10m threshold=2000 stream_rast=streams direction=dirs
r.stream.order stream_rast=streams dir=dirs horton=horton
r.mapcalc "horton3 = if(horton>2,horton,null())"
r.stream.distance stream=streams dir=dirs method=downstream distance=distance elevation=elevation.10m

Next, to perform the analysis we need write two text files: one with the definition of maps used in analysis and the definition of fuzzy sets for every map, and a second with fuzzy rules. For this example:

MAPS file example (text file):

Note: the raster map names are specified with a "%" character (here "% elevation" and "% distance" are the input maps). The single output map must be named "%_OUTPUT_", in the map file, but the actual raster will be assigned the name from the "output" option to "r.fuzzy.system" (in the example below this is "flood").

# flood.map
% elevation
$ low {right; 2,6; sshaped; 0; 1}
$ high {left; 2,6; sshaped; 0; 1}
% distance
$ near {right; 40,80; sshaped; 0; 1}
$ far {left; 40,80; sshaped; 0; 1}
#output map
% _OUTPUT_
$ unprob {both; 0,20,20,40; linear; 0;1}
$ prob {both; 20,40,40,60; linear; 0;1}
$ veryprob {both; 40,60,60,80; linear; 0;1}

RULES file example (text file):

# flood.rul
$ unprob {elevation = high & distance = far}
$ prob {distance = near | elevation = low}
$ veryprob {distance = near & elevation = low}

Finally we need run r.fuzzy.system:

r.fuzzy.system maps=flood.map rules=flood.rul output=flood

The resulting map should look like the image below. Yellow colour means no risk, red high risk, green, blue end so on moderate risk.

REFERENCES

Jasiewicz, J. (2011). A new GRASS GIS fuzzy inference system for massive data analysis. Computers & Geosciences (37) 1525-1531. DOI https://doi.org/10.1016/j.cageo.2010.09.008
Zadeh, L.A. (1965). "Fuzzy sets". Information and Control 8 (3): 338-353. DOI:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958.
Novák, V. (1989). Fuzzy Sets and Their Applications. Bristol: Adam Hilger. ISBN 0-85274-583-4.
Klir, George J.; Yuan, Bo (1995). Fuzzy sets and fuzzy logic: theory and applications. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-101171-5.
Klir, George J.; St Clair, Ute H.; Yuan, Bo (1997). Fuzzy set theory: foundations and applications. Englewood Cliffs, NJ: Prentice Hall. ISBN 0133410587.
Meyer D, Hornik K (2009a). Generalized and Customizable Sets in R. Journal of Statistical Software, 31(2), 1-27. DOI DOI:10.18637/jss.v031.i02
Meyer D, Hornik K (2009b). sets: Sets, Generalized Sets, and Customizable Sets. R~package version~1.0, URL http://CRAN.R-project.org/package=sets.

AUTHOR

Jarek Jasiewicz

SOURCE CODE

Available at: r.fuzzy.system source code (history)

Latest change: Monday Jun 28 07:54:09 2021 in commit: 1cfc0af029a35a5d6c7dae5ca7204d0eb85dbc55