NAME
r.series.lwr - Approximates a time series and creates approximated, gap-filled output.KEYWORDS
raster, series, filteringSYNOPSIS
Flags:
- -l
- Reject low outliers
- -h
- Reject high outliers
- -z
- Don't keep files open
- -i
- Do not extrapolate, only interpolate
- --help
- Print usage summary
- --verbose
- Verbose module output
- --quiet
- Quiet module output
- --ui
- Force launching GUI dialog
Parameters:
- input=name[,name,...]
- Name of input raster map(s)
- file=name
- Input file with raster map names, one per line
- suffix=string
- Suffix for output maps
- The suffix will be appended to input map names
- Default: _lwr
- order=integer
- order number
- Order of the polynomial fitting function, 0 means weighted average
- Options: 0, 1, 2, 3
- Default: 1
- weight=string
- Weighing kernel function
- Options: uniform, triangular, epanechnikov, quartic, tricube, cosine
- Default: tricube
- fet=float
- Fit error tolerance
- dod=integer
- Degree of over-determination
- Default: 0
- range=lo,hi
- Ignore values outside this range
- time_steps=float[,float,...]
- Time steps of the input maps
- maxgap=float
- Maximum gap size to be interpolated
- delta=float
- Threshold for high amplitudes
- Delta should be between 0 and 1
- Default: 0
Table of contents
DESCRIPTION
r.series.lwr performs a local weighted regression (LWR, Cleveland and Devlin 1988) of time series in order to estimate missing values and identify outliers. For each input map, an output map with the suffix suffix (default: _lwr) is created.For each observation in the time series, the (in time) neighboring values are used to estimate a polynomial function that best fits the observations. The values are weighted according to their distance (in time) to the current observation. Values that are farther away in time get lower weights. The main difference among the different weight funtions lies in how strongly the current observation is emphasized with respect to its temporal neighbors. See this dedicated wiki for further details.
The option order determines the order of the polynomial function used to fit the observations. An order of 0 is a weighted average, an order of 1 is a linear regression. Recommended and default is order=2. An order of 3 might cause over-fitting, resulting in no smoothing, and should only be used with data that show high fluctuations.
The delta option is experimental. It smoothes the polynomial function. With a high delta value, a higher order polynomial function fitting becomes similar to a moving average.
Optionally, low and/or high outliers can be removed when fitting a polynomial by means of the -l and -h flags, respectively. In this case, a fit error tolerance (option fet) must be provided. The value of fet is relative to the value range of the variable being considered. The use of these flags will slow down the module and they are only needed when the time series contains many outliers. A few outliers are handled well with the default settings.
All gaps in the time series are by default interpolated, as long as the time series contains sufficient non-NULL observations. Optionally, the maximum size of gaps to be interpolated can be set with the maxgap option. The units of maxgap are the units of the time steps.
Extrapolation can be avoided with the -i flag. In this case, LWR is performed only from the first to the last non-NULL observation in the time series.
The module uses an adaptive bandwidth to fit the polynomial and searches for order + 1 + dod valid values around the current observation. The degree of over-determination (dod) is the user defined number of extra temporal neighbours that should be considered for the estimation of the value at each time step.
There is a trade-off between the goodness of fit to existing/original data and avoiding overshoots in gaps. This trade-off can be observed in the example below when order=2 is used along with dod=0. In this case, the reconstruction will most of the time be an exact match to the input data because LWR will try to copy the slopes in the data, including those very steep slopes, but this might create overshootings in gaps. The risk of overshootings can be alleviated by increasing dod (i.e. dod > 0), which will smooth the output. The effect of a dod=5 can be observed in the examples below.
NOTES
If the range option is given, all the values falling outside the low,high thresholds will be treated as if they were NULL.The low,high thresholds are floating point. Therefore, use -inf or inf for a single threshold (e.g., range=0,inf to ignore negative values, or range=-inf,-200.4 to ignore values above -200.4).
There is no need to give time steps if the time interval among maps is constant. If the interval is not constant, the user needs to assign time steps. These must always increase (i.e.: each time step must be larger than the previous one) and the total number of time steps must be equal to the number of input maps.
The maximum number of raster maps that can be processed is given by the user-specific limit of the operating system. For example, the soft limits for users are typically 1024. The soft limit can be changed with e.g. ulimit -n 4096 (UNIX-based operating systems) but it cannot be higher than the hard limit. If the latter is too low, you can as superuser add an entry in:
/etc/security/limits.conf # <domain> <type> <item> <value> your_username hard nofile 4096
cat /proc/sys/fs/file-max
Use the -z flag to analyze large amounts of raster maps without hitting open files limit and the file option to avoid hitting the size limit of command line arguments. Note that the computation using the file option is slower than with the input option. For every single row in the output map(s) all input maps are opened and closed. The amount of RAM will rise linearly with the number of specified input maps. The input and file options are mutually exclusive: the former is a comma separated list of raster map names and the latter is a text file with a new line separated list of raster map names. Note that the order of maps in one option or the other is very important.
EXAMPLES
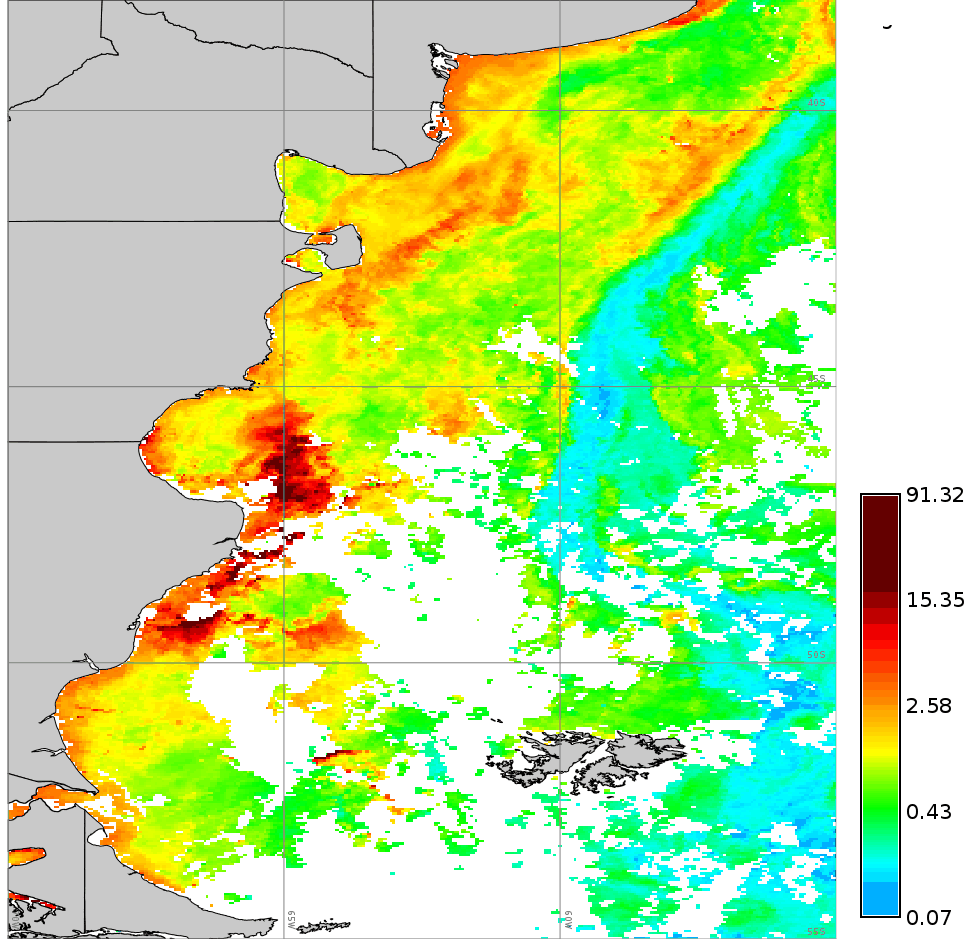
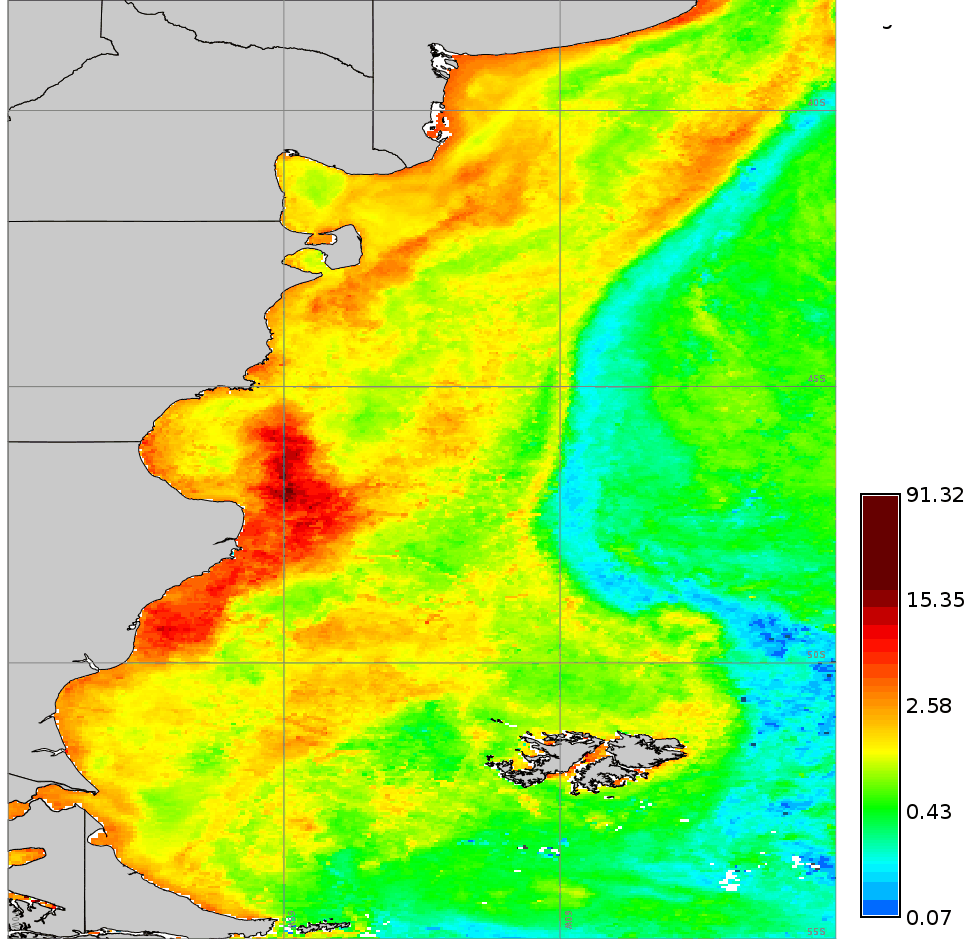
We use a time series of the Chlorophyll-a concentration level 3 product from MODIS Aqua (spatial resolution approx. 4 km and temporal resolution 8 days) to exemplify different parameter settings in r.series.lwr. We will first execute the module with default options to interpolate all existent gaps with a polynomial of first order (i.e. order=1). Second, we change to a second order polynomial (i.e. order=2). The third case shows how to use -l/-h flags in combination with fet to remove outliers. In this example we will remove only high outiliers (-h flag) and we set a value of fet relative to the values of Chlorophyll-a concentration. The fourth example demonstrates the use of dod to consider more time steps when fitting the polynomial at each observation (Note that the resulting series is smoother, i.e. the fluctuations have been smoothed). Finally, we set a value for maxgap, so that only temporal gaps equal to or smaller than the maximum gap will be interpolated.# list of maps maplist=`g.list type=raster pattern=A201[2-3]*chlor_a* sep=,` # 1. default settings (order=1) r.series.lwr input=$maplist suffix=_lwr1 order=1 weight=tricube # 2. change to order=2 r.series.lwr input=$maplist suffix=_lwr2 order=2 weight=tricube # 3. set degree of overdetermination (dod) to consider more time steps (smoothes the series) r.series.lwr -i input=$maplist suffix=_lwr3 order=2 weight=tricube dod=5 # 4. set dod > 1 and -h flag to identify and remove high outliers with fit error tolerance (fet=0.5) r.series.lwr -i -h input=$maplist suffix=_lwr4 order=2 weight=tricube dod=5 fet=0.5 # 5. set maxgap (temporal gaps longer than maxgap will not be filled) r.series.lwr -i input=$maplist suffix=_lwr5 order=2 weight=tricube maxgap=4
for i in `seq 1 5` ; do
# create time series with lwr outputs
t.create type=strds temporaltype=absolute output=cla_lwr${i} \
title="LWR output for Chl-a" \
description="MODIS Aqua L3 Chl-a 8-day 4km 2012-2013. Reconstruction with r.series.lwr - run ${i}"
# create list with filenames to parse
g.list type=raster pattern="*_lwr${i}" output=names_list_${i}
# parse filenames, convert YYYYDOY to YYYY-MM-DD and write file to use in t.register
for mapname in `cat names_list_${i}` ; do
year_start=`echo ${mapname:1:4}`
doy_start=`echo ${mapname:5:3}`
year_end=`echo ${mapname:8:4}`
doy_end=`echo ${mapname:12:3}`
# convert YYYY-DOY to YYYY-MM-DD
doy_start=`echo "$doy_start" | sed 's/^0*//'`
doy_end=`echo "$doy_end" | sed 's/^0*//'`
START_DATE=`date -d "${year_start}-01-01 +$(( ${doy_start} - 1 ))days" +%Y-%m-%d`
END_DATE=`date -d "${year_end}-01-01 +$(( ${doy_end} ))days" +%Y-%m-%d`
# print mapname, start and end date
echo "$mapname|$START_DATE|$END_DATE" >> map_list_start_and_end_time_${i}.txt
done
# register maps in strds
t.register input=cla_lwr${i} type=raster file=map_list_start_and_end_time_${i}.txt
# get info
t.info cla_lwr${i}
done
g.gui.tplot strds=cla_2012_2013 coordinates=-61.196485623,-45.3232161874 g.gui.tplot strds=cla_lwr1,cla_lwr2 coordinates=-61.196485623,-45.3232161874 g.gui.tplot strds=cla_lwr3,cla_lwr4 coordinates=-61.196485623,-45.3232161874 g.gui.tplot strds=cla_lwr5,cla_2012_2013 coordinates=-61.196485623,-45.3232161874
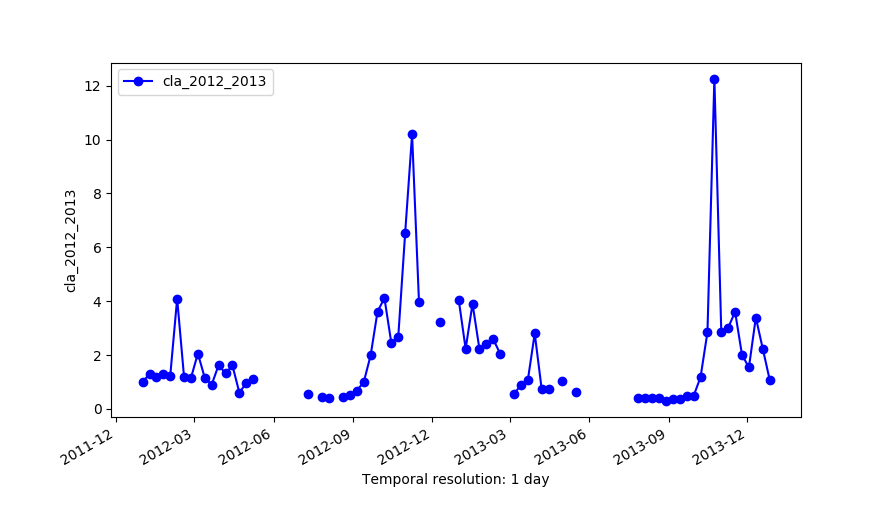
Original series (cla_2012_2013)
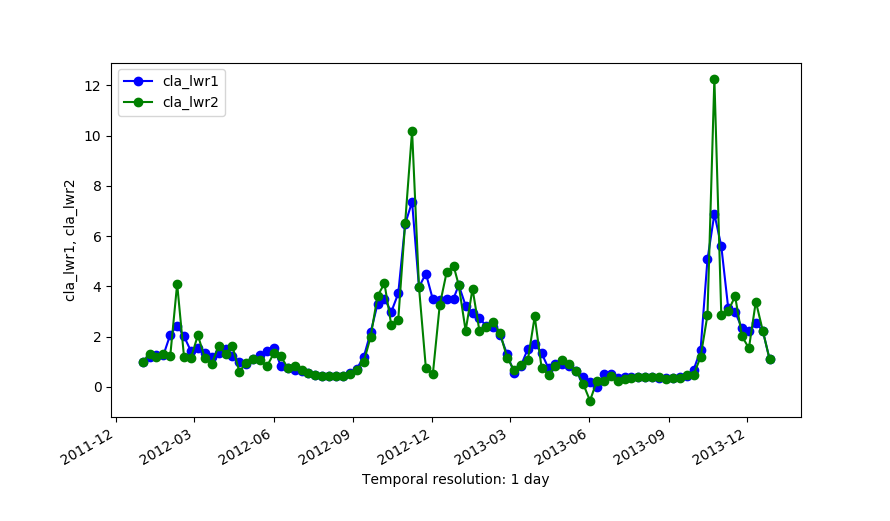
Outputs of LWR with order=1 (cla_lwr1) and order=2 (cla_lwr2).
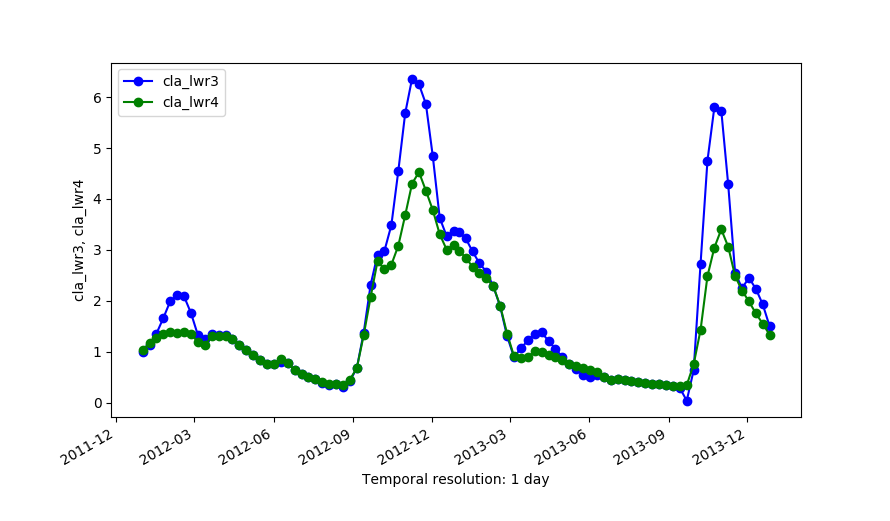
Outputs of LWR with dod=5 (cla_lwr3) and dod=5 plus -h flag and fet=0.5 (cla_lwr4).
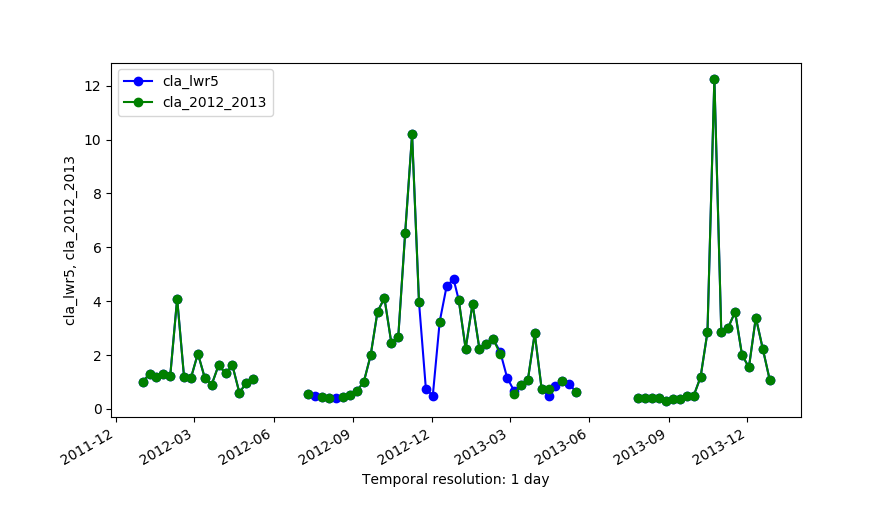
Original series (cla_2012_2013) and the output of LWR with maxgap=4 (cla_lwr5).
REFERENCES
Cleveland, William S.; Devlin, Susan J. (1988). Locally-Weighted Regression: An Approach to Regression Analysis by Local Fitting, Journal of the American Statistical Association, 83 (403), 596-610, doi:10.2307/2289282SEE ALSO
r.series, r.hantsAUTHOR
Markus MetzSOURCE CODE
Available at: r.series.lwr source code (history)
Latest change: Wed Feb 2 21:46:15 2022 in commit: 2e3dcb5eafe36d640aa68585be0192f07ca1eabb
Main index | Raster index | Topics index | Keywords index | Graphical index | Full index
© 2003-2022 GRASS Development Team, GRASS GIS 8.0.3dev Reference Manual