
NAME
v.qcount - Indices for quadrat counts of vector point lists.KEYWORDS
vector, statistics, point patternSYNOPSIS
Flags:
- -g
- Print results in shell script style
- --overwrite
- Allow output files to overwrite existing files
- --help
- Print usage summary
- --verbose
- Verbose module output
- --quiet
- Quiet module output
- --ui
- Force launching GUI dialog
Parameters:
- input=name [required]
- Name of input vector map
- Or data source for direct OGR access
- layer=string
- Layer number or name ('-1' for all layers)
- A single vector map can be connected to multiple database tables. This number determines which table to use. When used with direct OGR access this is the layer name.
- Default: -1
- output=name
- Name for output quadrat centers map (number of points is written as category)
- nquadrats=integer [required]
- Number of quadrats
- radius=float [required]
- Quadrat radius
Table of contents
DESCRIPTION
v.qcount computes six different quadrat count statistics that provide a measure of how much an user defined point pattern departs from a complete spatial random point pattern.Points are distributed following a complete spatial randomness (CSR) pattern if events are equally likely to occur anywhere within an area. There are two types departure from a CSR: regularity and clustering. Figure 1 gives an example of a complete random, regular and a clustered pattern.


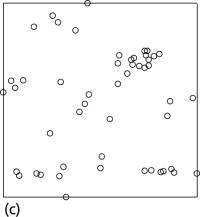
Figure 1: Realization of two-dimensional Poisson processes of 50 points on the unit square exhibiting (a) complete spatial randomness, (b) regularity, and (c) clustering.
Various indices and statistics measure departure from CSR. The v.qcount function implements six different quadrat count indices that are described in Cressie (1991; p. 590-591)[1] and in Ripley (1981; p. 102-106)[2] and summarized in Table 1.

Table 1: Indices for Quadrat Count Data. Adapted from Cressie [1], this table shows the statistics computed for the quadrats in Figure 2.
These indices are computed as follows: v.qcount chooses nquadrads circular quadrats of radius radius such that they are completely within the bounds of the current region and no two quadrats overlap. The number of points falling within each quadrat are counted and indices are calculated to estimate the departure of point locations from complete spatial randomness. This is illustrated in Figure 2.
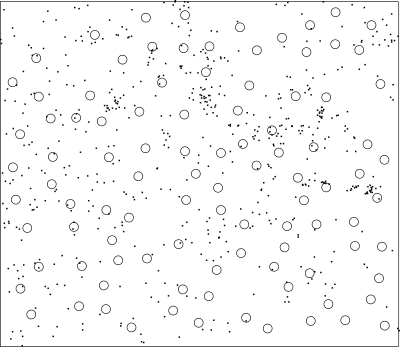
Figure 2: Randomly placed quadrats (n = 100) with 584 sample points.
The number of points is written as category to the output map (and not to an attribute table).
NOTES
This program may not work properly with lat-long data. It uses hypot() in two files: count.c and findquads.c.KNOWN ISSUES
Timestamp not working for header part of counts output. (2000-10-28)REFERENCES
General references include:[1] Noel A. C. Cressie. Statistics for Spatial Data. Wiley Series in Probability and Mathematical Statistics. John Wiley & Sons, New York, NY, 1st edition, 1991.
[2] Brian D. Ripley. Spatial Statistics. John Wiley \& Sons, New York, NY, 1981.
References to the indices include:
[3] R. A. Fisher, H. G. Thornton, and W. A. Mackenzie. The accuracy of the plating method of estimating the density of bacterial populations. Annals of Applied Biology, 9:325-359, 1922.
[4] F. N. David and P. G. Moore. Notes on contagious distributions in plant populations. Annals of Botany, 18:47-53, 1954.
[5] J. B. Douglas. Clustering and aggregation. Sankhya B, 37:398-417, 1975.
[6] M. Lloyd. Mean crowding. Journal of Animal Ecology, 36:1-30, 1967.
[7] M. Morista. Measuring the dispersion and analysis of distribution patterns. Memoires of the Faculty of Science, Kyushu University, Series E. Biology, 2:215-235, 1959.
A more detailed background is given in the tutorial:
[8] James Darrell McCauley 1993. Complete Spatial Randomness and Quadrat Methods - GRASS Tutorial on v.qcount
SEE ALSO
v.random, v.distance, v.neighbors, v.perturbAUTHORS
James Darrell McCauleywhen he was at: Agricultural Engineering Purdue University
Modified for GRASS 5.0 by Eric G. Miller (2000-10-28)
Modified for GRASS 5.7 by R. Blazek (2004-10-14)
SOURCE CODE
Available at: v.qcount source code (history)
Latest change: Monday Jan 30 09:36:46 2023 in commit: 0fb05e493f4ef73f4a721b019bffc357be2ec8d6
Main index | Vector index | Topics index | Keywords index | Graphical index | Full index
© 2003-2025 GRASS Development Team, GRASS GIS 8.4.3dev Reference Manual